Россия
Красноярск, Красноярский край, Россия
Красноярск, Красноярский край, Россия
Ключевой задачей данного исследования является поиск оптимальных решений в области размещения производственных мощностей и определения оптимального размера партии продукции. Рассматриваются методы, позволяющие минимизировать издержки, связанные с транспортировкой, хранением и производством, а также максимизировать эффективность использования ресурсов. Представлен анализ методов и алгоритмов, применяемых для оптимизации загрузки производственных мощностей: алгоритм Джонсона, метод ветвей и границ, генетический алгоритм. Каждый из методов исследуется с точки зрения их применимости, точности, вычислительной сложности и адаптивности к различным условиям производства. Уделено внимание сравнению сильных и слабых сторон каждого подхода, что позволяет оценить их эффективность в зависимости от специфики производственных процессов. Результаты проведенного анализа показывают, что классические методы остаются актуальными для задач с четко определенными параметрами и стабильными условиями, тогда как современные технологии, такие как нейронные сети, генетические алгоритмы и методы оптимизации на основе больших данных, демонстрируют высокую эффективность в условиях неопределенности, динамически изменяющихся требований и сложных производственных систем. На основе проведенного исследования предложены возможные направления дальнейшего развития, включая интеграцию классических и современных методов, разработку гибридных подходов, сочетающих в себе преимущества различных технологий.
производственные процессы, методы оптимизации, генетический алгоритм, метод ветвей и границ, алгоритм Джонсона, производственная мощность
Введение
Задача планирования загрузки производственных мощностей является одной из ключевых в управлении производством, особенно в условиях высокой конкуренции и необходимости минимизации временных затрат, переналадок и простоев оборудования. Для выполнения этой задачи используются различные подходы и алгоритмы оптимизации, каждый из которых отличается своими преимуществами и недостатками. Важную роль в решении задач планирования загрузки производственных мощностей играет комбинаторика, т. к. такие задачи часто сводятся к поиску оптимального распределения ресурсов среди множества возможных вариантов. Комбинаторика – это раздел математики, который изучает дискретные структуры, методы подсчета количества различных комбинаций объектов, а также их расположение и упорядочивание [1, 2]. Комбинаторные задачи, такие как распределение работ между станками или размещение деталей с учетом временных параметров и ограничений, предполагают детальный анализ всех возможных вариантов расстановки и последовательности выполнения операций. Эти задачи часто относятся к классу NP-трудных, что означает, что найти оптимальное решение за разумное время напрямую (перебором) невозможно при больших размерностях, поэтому для решения подобных задач применяются методы комбинаторной оптимизации, такие как метод ветвей и границ, генетические алгоритмы и другие эвристические подходы, которые позволяют эффективно исследовать пространство возможных решений и находить близкие к оптимальным варианты [3]. Таким образом, задача планирования загрузки производственных мощностей становится частью более широкого класса комбинаторных задач, где основной целью является минимизация функции целей при наличии жестких ограничений. Целью данного исследования является анализ и сравнение различных методов и алгоритмов оптимизации планирования производственных мощностей с точки зрения их применимости, точности, вычислительной сложности и адаптивности к условиям производства. Для анализа были выбраны алгоритм Джонсона, метод ветвей и границ и генетический алгоритм, поскольку они представляют различные классы подходов к решению задач оптимизации производственных процессов: алгоритм Джонсона – эффективный точный метод для двухстаночных задач, метод ветвей и границ – универсальный точный алгоритм, применимый к более широкому классу задач, а генетический алгоритм – современный эвристический метод, перспективный для задач большой размерности и динамических условий производства, что позволяет всесторонне оценить их эффективность и обосновать выбор метода в зависимости от специфики производственной среды.
Анализ методов планирования производственных мощностей
Рассмотрим задачу оптимизации загрузки производственных мощностей, которая формулируется следующим образом. Имеется n работ, которые должны быть выполнены на двух станках M1 и M2. Каждая работа i характеризуется временем ее выполнения на первом станке ai и временем выполнения на втором станке bi, где i = 1, 2, …, n. Каждая работа должна сначала выполниться на станке M1, а затем на станке M2. Станки могут работать параллельно, но одна работа не может начинаться на втором станке до тех пор, пока она полностью не завершена на первом. Порядок выполнения работ: P = (p1, p2, …, pn). Для решения поставленной задачи оптимизации загрузки производственных мощностей на двух станках воспользуемся алгоритмом Джонсона. Этот алгоритм позволяет эффективно находить оптимальную последовательность выполнения работ, минимизируя общее время завершения всех работ [4, 5].
Рассмотрим пример с 4 работами из табл. 1.
Таблица 1
Table 1
Исходные данные для четырех работ на двух станках
Source data for four jobs on two machines
|
Номер работы i |
Станок ai, с |
Станок bi, с |
|
1 |
3 |
6 |
|
2 |
5 |
2 |
|
3 |
1 |
4 |
|
4 |
6 |
8 |
Шаг 1. Разделение работ Jn на множества Sn:
– S1 = {J1, J3} (т. к. a1 ≤ b1 и a3 ≤ b3);
– S2 = {J2, J4} (т. к. a2 > b2 и a4 > b4).
Шаг 2. Упорядочивание множеств:
– S1 упорядочивается по возрастанию ai: J3, J1;
– S2 упорядочивается по убыванию bi: J4, J2.
Шаг 3. Формирование последовательности: итоговая последовательность: p = (J3, J1, J4, J2).
Шаг 4. Вычисление общего времени выполнения всех работ Cmax: построим график последовательности выполнения работ на станках M1 и M2 (табл. 2).
Таблица 2
Table 2
Последовательность выполнения работ на двух станках
The sequence of work performed on two machines
|
Время завершения работ, с |
Станок M1 |
Станок M2 |
|
0–1 |
J3 |
– |
|
1–4 |
J1 |
J3 |
|
4–10 |
J4 |
J1 |
|
10–12 |
J2 |
J4 |
|
12–14 |
– |
J2 |
Общее время завершения всех работ Cmax = 14 с.
Алгоритм Джонсона минимизирует простои на станке M2, что приводит к минимальному общему времени завершения. Он гарантирует оптимальное решение для двух станков, но не применим для большего числа станков. Далее попробуем решить сформулированную ранее задачу о 2-х станках и 4-х работах методом ветвей и границ. Он используется для нахождения оптимального решения путем систематического перебора всех возможных вариантов, но с отсечением заведомо неперспективных ветвей (подмножеств решений), что позволяет сократить объем вычислений [6, 7].
Математическая формулировка метода ветвей и границ: пусть:
– X – множество всех допустимых решений;
– f(x) – целевая функция, которую нужно минимизировать;
– x* – оптимальное решение, такое что f(x*) = min f(x).
Шаги алгоритма:
1. Инициализация:
– создать очередь подмножеств Q, начав с полного множества X;
– установить текущее лучшее решение x* = ∅ и f(x*) = + ∞.
2. Ветвление:
– извлечь подмножество Xi из очереди Q;
– разбить Xi на более мелкие подмножества Xi1, Xi2, …, Xik.
3. Оценка границ:
– для каждого подмножества Xij вычислить нижнюю и верхнюю границу;
– если нижняя граница Xij ≥ f(x*), отбросить Xij, иначе добавить Xij в очередь.
4. Завершение:
– повторять шаги 2–4, пока очередь Q не станет пустой;
– вернуть x* как оптимальное решение.
Рассмотрим данный пример с 4 работами из табл. 1.
Шаг 1. Инициализация:
– множество всех возможных последовательностей: X – все перестановки из 4-х работ (24 варианта);
– текущее лучшее решение x* = Ø и f(x*) = + ∞.
Шаг 2. Ветвление. Разбиваем X на подмножества по первой работе:
– X1: последовательности, начинающиеся с J1;
– X2: последовательности, начинающиеся с J2;
– X3: последовательности, начинающиеся с J3;
– X4: последовательности, начинающиеся с J4.
Шаг 3. Оценка границ. Для каждого подмножества вычисляем нижнюю границу LB (Xn):
– для X1: LB (X1) = a1 + min (b1, a2 + a3 + a4) = 3 + + min (6, 12) = 9;
– для X2: LB (X2) = a2 + min (b2, a1 + a3 + a4) = 5 + + min (2, 10) = 7;
– для X3: LB (X3) = a3 + min (b3, a1 + a2 + a4) = 1 + + min (4, 14) = 5;
– для X4: LB (X4) = a4 + min (b4, a1 + a2 + a3) = 6 + + min (8, 9) = 14.
Шаг 4. Отсечение. Для каждого подмножества повторяем шаги 2, 3.
Шаг 5. Нахождение оптимального решения.
После полного перебора и отсечения неперспективных ветвей находим оптимальную последовательность. В данном примере это P = (J3, J1, J4, J2) c Cmax = 14.
Метод ветвей и границ позволяет найти оптимальное решение, но требует значительных вычислительных ресурсов для больших задач. В данном примере он подтверждает результат, полученный алгоритмом Джонсона.
Теперь перейдем к решению той же задачи с использованием генетического алгоритма. Генетический алгоритм воспроизводит принципы естественного отбора и эволюции, чтобы находить оптимальные решения. Суть метода состоит в формировании популяции возможных решений, их отборе, скрещивании и мутации, что позволяет улучшать качество последующих поколений [8–10].
В данном случае хромосома представляет собой последовательность выполнения работ. Например, для 4-х работ хромосома может выглядеть так (3, 1, 4, 2), что означает порядок выполнения: J3, J1, J4, J2.
Фенотип – это общее время завершения всех работ (Cmax) для данной последовательности. Вычисляется путем моделирования выполнения работ на станках M1 и M2.
Операторы генетического алгоритма:
– селекция – выбор родительских хромосом с вероятностью, обратно пропорциональной их Cmax;
– скрещивание – создание потомков из двух родительских хромосом;
– мутация – случайное изменение порядка работ в хромосоме.
Критерии остановки:
– достижение максимального числа поколений;
– нахождение решения с Cmax, не превышающим заданное значение.
Пошаговое решение:
Шаг 1. Инициализация. Создаем начальную популяцию из 4-х хромосом:
– C1 = [1, 2, 3, 4], Cmax = 20;
– C2 = [1, 2, 3, 4], Cmax = 14;
– C3 = [1, 2, 3, 4], Cmax = 22;
– C4 = [1, 2, 3, 4], Cmax = 23.
Шаг 2. Селекция. Вычисляем вероятности выбора хромосом:
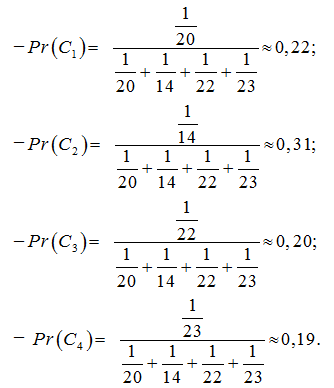
Выбираем две хромосомы для скрещивания C2 и C1.
Шаг 3. Скрещивание. Применяем частично отображаемое скрещивание:
– C1 = [1, 2, 3, 4], Cmax = 20;
– C2 = [3, 1, 4, 2], Cmax = 14;
– C3 = [3, 4, 1, 2], Cmax = 16;
– C4 = [1, 2, 3, 4], Cmax = 20.
Шаг 4. Проверка критериев остановки. Если достигнуто максимальное число поколений, завершаем алгоритм. Лучшее решение: (3, 1, 4, 2) с Cmax = 14.
Генетический алгоритм нашел оптимальную последовательность (3, 1, 4, 2) с общим временем завершения Cmax = 14. Это совпадает с решением, полученным алгоритмом Джонсона и методом ветвей и границ.
Результаты эксперимента
Для проведения экспериментов выбрана задача с фиксированным набором работ, где каждая работа характеризуется временем выполнения на станках M1 и M2. Такой подход позволяет наглядно сравнить результаты, полученные каждым алгоритмом, и оценить их эффективность по следующим критериям: время обработки и вероятность неправильного ответа.
Для подведения итогов исследования методов решения задачи о станках проведем тестирование наиболее эффективных алгоритмов на компьютере, оценивая их по следующим критериям: количество работ, время обработки и вероятность ошибки (табл. 3).
Таблица 3
Table 3
Сравнение алгоритмов
Comparison of algorithms
|
Количество работ |
Время обработки, c |
Вероятность ошибки, % |
Тип алгоритма |
|
Алгоритм Джонсона |
|||
|
10 |
0,0001 |
0 |
Точный |
|
32 |
0,0002 |
||
|
100 |
0,0013 |
||
|
Метод ветвей и границ |
|||
|
10 |
15 |
0 |
Точный |
|
32 |
900 |
||
|
100 |
более 900 |
||
|
Генетический алгоритм |
|||
|
10 |
0,17 |
1 |
Приближенный |
|
32 |
0,39 |
3 |
|
|
100 |
1,2 |
5 |
|
Алгоритм Джонсона применим лишь для специфических случаев с двумя станками и ограниченным числом заданий, поэтому его использование ограничено. Для задач с небольшим числом работ, где n < 10, оптимальным выбором может стать метод ветвей и границ, который гарантирует нахождение точного решения. Для задач с большим числом работ, где n > 10, предпочтительнее использовать генетический алгоритм, поскольку он обеспечивает приемлемую точность при значительно меньших затратах времени по сравнению с методом ветвей и границ.
Заключение
Представлен подробный анализ современных методов оптимизации загрузки производственных мощностей, таких как алгоритм Джонсона, метод ветвей и границ и генетический алгоритм. Все эти методы были применены к задаче минимизации общего времени завершения работ на двух станках, что позволило оценить их эффективность и выявить сильные и слабые стороны каждого подхода.
Экспериментальная проверка показала, что каждый из рассматриваемых методов обладает своими преимуществами и недостатками. Так, алгоритм Джонсона продемонстрировал свою эффективность для задач с двумя станками, обеспечивая быстрое нахождение оптимального решения. Однако его применимость ограничена случаями с двумя станками, что делает его менее универсальным для более сложных производственных процессов. Метод ветвей и границ обеспечил точное решение, но его высокая вычислительная сложность сделала его непригодным для задач большого объема.
Наиболее эффективным оказался генетический алгоритм, который показал стабильность в нахождении высококачественных решений даже для задач средней и большой размерности. Хотя генетический алгоритм не гарантирует нахождения глобального оптимума, его способность быстро адаптироваться и улучшать решения делает его предпочтительным для большинства практических ситуаций.
Таким образом, статья предоставляет полезную информацию для специалистов в области управления производством, помогая сделать обоснованный выбор метода оптимизации в зависимости от особенностей конкретной производственной среды. Полученные в исследовании результаты будут использованы для разработки нового гибридного алгоритма оптимизации загрузки производственных мощностей, сочетающего точные и эвристические методы, что обеспечит высокую эффективность и адаптивность в условиях сложных и динамически изменяющихся производственных систем.
1. Алексеев О. Г. Основы комбинаторики: учеб. М.: Наука, 1995. 456 с.
2. Аллаберенов С. А. Комбинаторика и ее роль в дискретной математике // Вестн. науки. 2024. Т. 5. № 9 (78). С. 419–423.
3. Гэри М. Р., Джонсон Д. С. Компьютеры и трудно-решаемость: руководство по теории NP-полноты. М.: Мир, 1982. 416 с.
4. Джавадов А. А. Теория расписаний и алгоритм Джонсона // Журн. математ. кибернетики. Ташкент: Мир математики, 1966. № 2. С. 25–32.
5. Андреева И. А. Обзор эвристических алгоритмов для решения задачи Джонсона // Программно-техническое обеспечение автоматизированных систем: материалы Всерос. молодеж. науч.-практ. конф. (Барнаул, 23 ноября 2023 г.). Барнаул: Изд-во Алтайс. гос. техн. ун-та им. И. И. Ползунова, 2023. С. 8–12.
6. Шемчук Г. Д. Эвристические алгоритмы в программировании: метод ближайшего соседа и метод ветвей и границ // Научному прогрессу – творчество молодых. 2024. № 1. С. 796–798.
7. Клоков С. А. Метод ветвей и границ для решения задачи о коммивояжёре // Молодой ученый. 2021. № 2 (344). С. 21–23.
8. Мельников Б. Ф. Генетические алгоритмы: основы и приложения. М.: Физматлит, 2008. 320 с.
9. Загинайло М. В. Генетический алгоритм как эффективный инструмент эволюционных алгоритмов // Инновации. Наука. Образование. 2020. № 22. С. 513–518.
10. Сохраби М. Алгоритм генетической инженерии (GEA): эффективный метаэвристический алгоритм для решения задач комбинаторной оптимизации // Автома-тика и телемеханика. 2024. № 3. С. 23–37.