Russian Federation
Krasnoyarsk, Krasnoyarsk, Russian Federation
Krasnoyarsk, Krasnoyarsk, Russian Federation
The key objective of this study is to find optimal solutions in the field of production capacity allocation and determining the optimal batch size. Methods are considered to minimize the costs associated with transportation, storage and production, as well as maximize the efficiency of resource use. The analysis of methods and algorithms used to optimize production capacity utilization is presented: Johnson's algorithm, the method of branches and boundaries, and the genetic algorithm. Each of the methods is being investigated in terms of their applicability, accuracy, computational complexity, and adaptability to different production conditions. Attention is paid to comparing the strengths and weaknesses of each approach, which makes it possible to evaluate their effectiveness depending on the specifics of production processes. The results of the analysis show that classical methods remain relevant for tasks with well-defined parameters and stable conditions, while modern technologies such as neural networks, genetic algorithms and optimization methods based on big data demonstrate high efficiency in conditions of uncertainty, dynamically changing requirements and complex production systems. Based on the conducted research, possible directions for further development are proposed, including the integration of classical and modern methods, the development of hybrid approaches combining the advantages of various technologies.
production processes, optimization methods, genetic algorithm, branch and bound method, Johnson algorithm, production capacity
Введение
Задача планирования загрузки производственных мощностей является одной из ключевых в управлении производством, особенно в условиях высокой конкуренции и необходимости минимизации временных затрат, переналадок и простоев оборудования. Для выполнения этой задачи используются различные подходы и алгоритмы оптимизации, каждый из которых отличается своими преимуществами и недостатками. Важную роль в решении задач планирования загрузки производственных мощностей играет комбинаторика, т. к. такие задачи часто сводятся к поиску оптимального распределения ресурсов среди множества возможных вариантов. Комбинаторика – это раздел математики, который изучает дискретные структуры, методы подсчета количества различных комбинаций объектов, а также их расположение и упорядочивание [1, 2]. Комбинаторные задачи, такие как распределение работ между станками или размещение деталей с учетом временных параметров и ограничений, предполагают детальный анализ всех возможных вариантов расстановки и последовательности выполнения операций. Эти задачи часто относятся к классу NP-трудных, что означает, что найти оптимальное решение за разумное время напрямую (перебором) невозможно при больших размерностях, поэтому для решения подобных задач применяются методы комбинаторной оптимизации, такие как метод ветвей и границ, генетические алгоритмы и другие эвристические подходы, которые позволяют эффективно исследовать пространство возможных решений и находить близкие к оптимальным варианты [3]. Таким образом, задача планирования загрузки производственных мощностей становится частью более широкого класса комбинаторных задач, где основной целью является минимизация функции целей при наличии жестких ограничений. Целью данного исследования является анализ и сравнение различных методов и алгоритмов оптимизации планирования производственных мощностей с точки зрения их применимости, точности, вычислительной сложности и адаптивности к условиям производства. Для анализа были выбраны алгоритм Джонсона, метод ветвей и границ и генетический алгоритм, поскольку они представляют различные классы подходов к решению задач оптимизации производственных процессов: алгоритм Джонсона – эффективный точный метод для двухстаночных задач, метод ветвей и границ – универсальный точный алгоритм, применимый к более широкому классу задач, а генетический алгоритм – современный эвристический метод, перспективный для задач большой размерности и динамических условий производства, что позволяет всесторонне оценить их эффективность и обосновать выбор метода в зависимости от специфики производственной среды.
Анализ методов планирования производственных мощностей
Рассмотрим задачу оптимизации загрузки производственных мощностей, которая формулируется следующим образом. Имеется n работ, которые должны быть выполнены на двух станках M1 и M2. Каждая работа i характеризуется временем ее выполнения на первом станке ai и временем выполнения на втором станке bi, где i = 1, 2, …, n. Каждая работа должна сначала выполниться на станке M1, а затем на станке M2. Станки могут работать параллельно, но одна работа не может начинаться на втором станке до тех пор, пока она полностью не завершена на первом. Порядок выполнения работ: P = (p1, p2, …, pn). Для решения поставленной задачи оптимизации загрузки производственных мощностей на двух станках воспользуемся алгоритмом Джонсона. Этот алгоритм позволяет эффективно находить оптимальную последовательность выполнения работ, минимизируя общее время завершения всех работ [4, 5].
Рассмотрим пример с 4 работами из табл. 1.
Таблица 1
Table 1
Исходные данные для четырех работ на двух станках
Source data for four jobs on two machines
|
Номер работы i |
Станок ai, с |
Станок bi, с |
|
1 |
3 |
6 |
|
2 |
5 |
2 |
|
3 |
1 |
4 |
|
4 |
6 |
8 |
Шаг 1. Разделение работ Jn на множества Sn:
– S1 = {J1, J3} (т. к. a1 ≤ b1 и a3 ≤ b3);
– S2 = {J2, J4} (т. к. a2 > b2 и a4 > b4).
Шаг 2. Упорядочивание множеств:
– S1 упорядочивается по возрастанию ai: J3, J1;
– S2 упорядочивается по убыванию bi: J4, J2.
Шаг 3. Формирование последовательности: итоговая последовательность: p = (J3, J1, J4, J2).
Шаг 4. Вычисление общего времени выполнения всех работ Cmax: построим график последовательности выполнения работ на станках M1 и M2 (табл. 2).
Таблица 2
Table 2
Последовательность выполнения работ на двух станках
The sequence of work performed on two machines
|
Время завершения работ, с |
Станок M1 |
Станок M2 |
|
0–1 |
J3 |
– |
|
1–4 |
J1 |
J3 |
|
4–10 |
J4 |
J1 |
|
10–12 |
J2 |
J4 |
|
12–14 |
– |
J2 |
Общее время завершения всех работ Cmax = 14 с.
Алгоритм Джонсона минимизирует простои на станке M2, что приводит к минимальному общему времени завершения. Он гарантирует оптимальное решение для двух станков, но не применим для большего числа станков. Далее попробуем решить сформулированную ранее задачу о 2-х станках и 4-х работах методом ветвей и границ. Он используется для нахождения оптимального решения путем систематического перебора всех возможных вариантов, но с отсечением заведомо неперспективных ветвей (подмножеств решений), что позволяет сократить объем вычислений [6, 7].
Математическая формулировка метода ветвей и границ: пусть:
– X – множество всех допустимых решений;
– f(x) – целевая функция, которую нужно минимизировать;
– x* – оптимальное решение, такое что f(x*) = min f(x).
Шаги алгоритма:
1. Инициализация:
– создать очередь подмножеств Q, начав с полного множества X;
– установить текущее лучшее решение x* = ∅ и f(x*) = + ∞.
2. Ветвление:
– извлечь подмножество Xi из очереди Q;
– разбить Xi на более мелкие подмножества Xi1, Xi2, …, Xik.
3. Оценка границ:
– для каждого подмножества Xij вычислить нижнюю и верхнюю границу;
– если нижняя граница Xij ≥ f(x*), отбросить Xij, иначе добавить Xij в очередь.
4. Завершение:
– повторять шаги 2–4, пока очередь Q не станет пустой;
– вернуть x* как оптимальное решение.
Рассмотрим данный пример с 4 работами из табл. 1.
Шаг 1. Инициализация:
– множество всех возможных последовательностей: X – все перестановки из 4-х работ (24 варианта);
– текущее лучшее решение x* = Ø и f(x*) = + ∞.
Шаг 2. Ветвление. Разбиваем X на подмножества по первой работе:
– X1: последовательности, начинающиеся с J1;
– X2: последовательности, начинающиеся с J2;
– X3: последовательности, начинающиеся с J3;
– X4: последовательности, начинающиеся с J4.
Шаг 3. Оценка границ. Для каждого подмножества вычисляем нижнюю границу LB (Xn):
– для X1: LB (X1) = a1 + min (b1, a2 + a3 + a4) = 3 + + min (6, 12) = 9;
– для X2: LB (X2) = a2 + min (b2, a1 + a3 + a4) = 5 + + min (2, 10) = 7;
– для X3: LB (X3) = a3 + min (b3, a1 + a2 + a4) = 1 + + min (4, 14) = 5;
– для X4: LB (X4) = a4 + min (b4, a1 + a2 + a3) = 6 + + min (8, 9) = 14.
Шаг 4. Отсечение. Для каждого подмножества повторяем шаги 2, 3.
Шаг 5. Нахождение оптимального решения.
После полного перебора и отсечения неперспективных ветвей находим оптимальную последовательность. В данном примере это P = (J3, J1, J4, J2) c Cmax = 14.
Метод ветвей и границ позволяет найти оптимальное решение, но требует значительных вычислительных ресурсов для больших задач. В данном примере он подтверждает результат, полученный алгоритмом Джонсона.
Теперь перейдем к решению той же задачи с использованием генетического алгоритма. Генетический алгоритм воспроизводит принципы естественного отбора и эволюции, чтобы находить оптимальные решения. Суть метода состоит в формировании популяции возможных решений, их отборе, скрещивании и мутации, что позволяет улучшать качество последующих поколений [8–10].
В данном случае хромосома представляет собой последовательность выполнения работ. Например, для 4-х работ хромосома может выглядеть так (3, 1, 4, 2), что означает порядок выполнения: J3, J1, J4, J2.
Фенотип – это общее время завершения всех работ (Cmax) для данной последовательности. Вычисляется путем моделирования выполнения работ на станках M1 и M2.
Операторы генетического алгоритма:
– селекция – выбор родительских хромосом с вероятностью, обратно пропорциональной их Cmax;
– скрещивание – создание потомков из двух родительских хромосом;
– мутация – случайное изменение порядка работ в хромосоме.
Критерии остановки:
– достижение максимального числа поколений;
– нахождение решения с Cmax, не превышающим заданное значение.
Пошаговое решение:
Шаг 1. Инициализация. Создаем начальную популяцию из 4-х хромосом:
– C1 = [1, 2, 3, 4], Cmax = 20;
– C2 = [1, 2, 3, 4], Cmax = 14;
– C3 = [1, 2, 3, 4], Cmax = 22;
– C4 = [1, 2, 3, 4], Cmax = 23.
Шаг 2. Селекция. Вычисляем вероятности выбора хромосом:
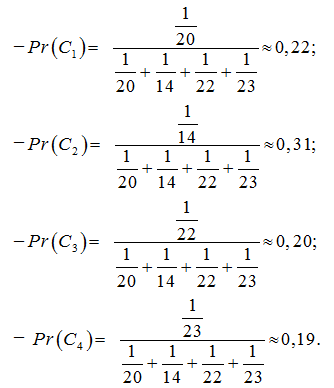
Выбираем две хромосомы для скрещивания C2 и C1.
Шаг 3. Скрещивание. Применяем частично отображаемое скрещивание:
– C1 = [1, 2, 3, 4], Cmax = 20;
– C2 = [3, 1, 4, 2], Cmax = 14;
– C3 = [3, 4, 1, 2], Cmax = 16;
– C4 = [1, 2, 3, 4], Cmax = 20.
Шаг 4. Проверка критериев остановки. Если достигнуто максимальное число поколений, завершаем алгоритм. Лучшее решение: (3, 1, 4, 2) с Cmax = 14.
Генетический алгоритм нашел оптимальную последовательность (3, 1, 4, 2) с общим временем завершения Cmax = 14. Это совпадает с решением, полученным алгоритмом Джонсона и методом ветвей и границ.
Результаты эксперимента
Для проведения экспериментов выбрана задача с фиксированным набором работ, где каждая работа характеризуется временем выполнения на станках M1 и M2. Такой подход позволяет наглядно сравнить результаты, полученные каждым алгоритмом, и оценить их эффективность по следующим критериям: время обработки и вероятность неправильного ответа.
Для подведения итогов исследования методов решения задачи о станках проведем тестирование наиболее эффективных алгоритмов на компьютере, оценивая их по следующим критериям: количество работ, время обработки и вероятность ошибки (табл. 3).
Таблица 3
Table 3
Сравнение алгоритмов
Comparison of algorithms
|
Количество работ |
Время обработки, c |
Вероятность ошибки, % |
Тип алгоритма |
|
Алгоритм Джонсона |
|||
|
10 |
0,0001 |
0 |
Точный |
|
32 |
0,0002 |
||
|
100 |
0,0013 |
||
|
Метод ветвей и границ |
|||
|
10 |
15 |
0 |
Точный |
|
32 |
900 |
||
|
100 |
более 900 |
||
|
Генетический алгоритм |
|||
|
10 |
0,17 |
1 |
Приближенный |
|
32 |
0,39 |
3 |
|
|
100 |
1,2 |
5 |
|
Алгоритм Джонсона применим лишь для специфических случаев с двумя станками и ограниченным числом заданий, поэтому его использование ограничено. Для задач с небольшим числом работ, где n < 10, оптимальным выбором может стать метод ветвей и границ, который гарантирует нахождение точного решения. Для задач с большим числом работ, где n > 10, предпочтительнее использовать генетический алгоритм, поскольку он обеспечивает приемлемую точность при значительно меньших затратах времени по сравнению с методом ветвей и границ.
Заключение
Представлен подробный анализ современных методов оптимизации загрузки производственных мощностей, таких как алгоритм Джонсона, метод ветвей и границ и генетический алгоритм. Все эти методы были применены к задаче минимизации общего времени завершения работ на двух станках, что позволило оценить их эффективность и выявить сильные и слабые стороны каждого подхода.
Экспериментальная проверка показала, что каждый из рассматриваемых методов обладает своими преимуществами и недостатками. Так, алгоритм Джонсона продемонстрировал свою эффективность для задач с двумя станками, обеспечивая быстрое нахождение оптимального решения. Однако его применимость ограничена случаями с двумя станками, что делает его менее универсальным для более сложных производственных процессов. Метод ветвей и границ обеспечил точное решение, но его высокая вычислительная сложность сделала его непригодным для задач большого объема.
Наиболее эффективным оказался генетический алгоритм, который показал стабильность в нахождении высококачественных решений даже для задач средней и большой размерности. Хотя генетический алгоритм не гарантирует нахождения глобального оптимума, его способность быстро адаптироваться и улучшать решения делает его предпочтительным для большинства практических ситуаций.
Таким образом, статья предоставляет полезную информацию для специалистов в области управления производством, помогая сделать обоснованный выбор метода оптимизации в зависимости от особенностей конкретной производственной среды. Полученные в исследовании результаты будут использованы для разработки нового гибридного алгоритма оптимизации загрузки производственных мощностей, сочетающего точные и эвристические методы, что обеспечит высокую эффективность и адаптивность в условиях сложных и динамически изменяющихся производственных систем.
1. Alekseev O. G. Osnovy kombinatoriki: uchebnik [Fundamentals of Combinatorics: a textbook]. Moscow, Nauka Publ., 1995. 456 p.
2. Allaberenov S. A. Kombinatorika i ee rol' v diskretnoi matematike [Combinatorics and its role in discrete mathematics]. Vestnik nauki, 2024, vol. 5, no. 9 (78), pp. 419-423.
3. Geri M. R., Dzhonson D. S. Komp'iutery i trud-noreshaemost': rukovodstvo po teorii NP-polnoty [Computers and Intractability: A Guide to NP-completeness Theory]. Moscow, Mir Publ., 1982. 416 p.
4. Dzhavadov A. A. Teoriia raspisanii i algoritm Dzhonsona [Timetable theory and Johnson's algorithm]. Zhurnal matematicheskoi kibernetiki. Tashkent, Mir matematiki Publ., 1966. No. 2. Pp. 25-32.
5. Andreeva I. A. Obzor evristicheskikh algoritmov dlia resheniia zadachi Dzhonsona [An overview of heuristic algorithms for solving the Johnson problem]. Programmno-tekhnicheskoe obespechenie avtomatizirovannykh sistem: materialy Vserossiiskoi molodezhnoi nauchno-prakticheskoi konferentsii (Barnaul, 23 noiabria 2023 g.). Barnaul, Izd-vo Altais. gos. tekhn. un-ta im. I. I. Polzunova, 2023. Pp. 8-12.
6. Shemchuk G. D. Evristicheskie algoritmy v programmirovanii: metod blizhaishego soseda i metod vetvei i granits [Heuristic algorithms in programming: the nearest neighbor method and the branch and boundary method]. Nauchnomu progressu – tvorchestvo molodykh, 2024, no. 1, pp. 796-798.
7. Klokov S. A. Metod vetvei i granits dlia resheniia zadachi o kommivoiazhere [The branch and boundary method for solving the traveling salesman problem]. Molodoi uchenyi, 2021, no. 2 (344), pp. 21-23.
8. Mel'nikov B. F. Geneticheskie algoritmy: osnovy i prilozheniia [Genetic algorithms: fundamentals and applications]. Moscow, Fizmatlit Publ., 2008. 320 p.
9. Zaginailo M. V. Geneticheskii algoritm kak effek-tivnyi instrument evoliutsionnykh algoritmov [The genetic algorithm as an effective tool of evolutionary algorithms]. Innovatsii. Nauka. Obrazovanie, 2020, no. 22, pp. 513-518.
10. Sokhrabi M. Algoritm geneticheskoi inzhenerii (GEA): effektivnyi metaevristicheskii algoritm dlia resheniia zadach kombinatornoi optimizatsii [Genetic Engineering Algorithm (GEA): an efficient metaheuristic algorithm for solving combinatorial optimization problems]. Avtomatika i telemekhanika, 2024, no. 3, pp. 23-37.