Россия
Исследуется задача построения оценок достоверности контроля технического состояния парка сложных технических систем (СТС) с метрологическим обеспечением. Используемая классическая полумарковская стационарная модель функционирования СТС включает следующие технические состояния: работо-способное, отказ, поверка отказавшего образца СТС, поверка работоспособного образца, состояние ложного отказа, состояние необнаруженного отказа, восстановление (ремонт). Основным показателем эффективности парка СТС является коэффициент готовности к применению по назначению. Для поддержания коэффициента готовности на высоком уровне в штатном режиме при эксплуатации парка проводятся периодические поверки с оптимальной периодичностью и оптимальным допуском на контролируемый параметр. Для оценки достоверности нахождения СТС в указанных состояниях предложены четыре показателя: правильность, точность, полнота и F1-метрика, которые используются в теории искусственного интеллекта как метрики бинарного классификатора. Проведено моделирование процессов функционирования парка СТС в разных режимах и при разных условиях. Показано влияние интервала между поверками, допуска на контролируемый параметр, интенсивности отказов и времени восстановления на показатели достоверности и на коэффициент готовности. Применение показателей достоверности позволит оператору парка СТС с метрологическим обеспечением комплексно анализировать актуальную оперативную информацию о текущем состоянии парка, разрабатывать и применять стратегии управления парком в зависимости от сложившейся на данный момент ситуации. Полученные результаты могут быть внедрены и использованы в системе поддержки принятия решения при оперативном дистанционном управлении парком СТС.
бинарный классификатор, достоверность контроля состояния, полумарковская модель, метрологическое обеспечение, сложная техническая система
Введение
В настоящее время в разных сферах деятельности широко применяются сложные технические системы (СТС) [1–3], в том числе и дистанционно управляемые оператором системы с метрологическим обеспечением (МО), которые подлежат периодическому метрологическому обслуживанию. В зависимости от конкретной решаемой задачи, а также от наличия различных возмущающих (мешающих) факторов МО может происходить как в штатной, так и внештатной ситуации (с оптимальной периодичностью и оптимальным допуском на контролируемый определяющий параметр (ОП) или с отличающимися от оптимальных значений параметрами поверки. Оператор, принимающий оперативное решение по управлению парком таких СТС, нуждается в достоверной и, по возможности, полной информации о техническом состоянии парка СТС, которая должна актуализироваться по мере появления новой информации.
Основным показателем эффективности парка СТС с МО является коэффициент готовности к применению [1, 4]. С целью поддержания коэффициента готовности на высоком уровне проводятся периодические поверки, суть которых заключается в контроле нахождения ОП СТС в требуемых пределах. Если в результате поверки выявляется, что ОП образца СТС вышел за допустимые пределы, производится восстановление (ремонт) соответствующего образца СТС, в результате которого ОП вновь попадает в требуемый допустимый диапазон.
В силу случайного характера изменения ОП и погрешности его измерения результаты контроля состояния (поверки) имеют случайный характер и могут быть определены лишь с некоторой достоверностью.
В настоящей работе предлагается в дополнение к традиционным в метрологии показателям достоверности (α – условная вероятность ложного отказа, β – условная вероятность необнаруженного отказа при поверке) использовать еще 4 показателя достоверности: правильность, точность, полноту и F1-меру, которые широко применяются в теории искусственного интеллекта как метрики бинарного классификатора [5–7]. Указанные 4 показателя комплексно характеризуют текущее состояние парка СТС с МО в части достоверности контроля технического состояния, функционирующего достаточно продолжительное время (в стационарном режиме).
Целью введения новых показателей (метрик) при моделировании МО парка СТС является обеспечение оператора актуальной, полной и достоверной информацией, отражающей не только результаты периодически проводимых поверок, но и информацией о текущем стационарном состоянии парка СТС в целом, которая характеризуется стационарными вероятностями нахождения образцов парка СТС в возможных технических состояниях [1, 4]. Так, для классической полумарковской стационарной модели основными состояниями являются работоспособное состояние, состояние отказа, поверка работоспособной СТС, поверка отказавшей СТС, состояние необнаруженного отказа, состояние ложного отказа, восстановление (ремонт).
Предлагаемые показатели достоверности являются функциями от вероятностей нахождения парка СТС в указанных семи технических состояниях. Они имеют интуитивно понятную интерпретацию, комплексно (разносторонне) характеризуют состояние парка и предназначены для принятия обоснованных решений оператором.
Методы
Описание метрик бинарного классификатора. Распространенными метриками бинарного классификатора являются правильность (accuracy), точность (precision), полнота (recall) и F1-мepа [5, 6]. Правильность представляет собой пропорцию верно предсказанных наблюдений:
где ТР (true positive, количество истинноположительных предсказаний – это наблюдения, которые относятся к положительному классу (работоспособное) и были предсказаны классификатором корректно); TN (true negative, количество истинноотрицательных предсказаний – это наблюдения, которые относятся к отрицательному классу (наличие отказа) и были предсказаны корректно); FP (false positive, количество ложноположительных предсказаний, также называемых ошибкой первого рода, – это наблюдения, которые были отнесены к неисправному классу, тогда как на практике относятся к исправному); FN (false negative, количество ложноотрицательных предсказаний, также называемых ошибкой второго рода, – это наблюдения, которые были отнесены к работоспособному классу, тогда как на практике относятся к неработоспособному). Удобство использования показателя правильности объясняется лаконичностью его значения: это отношение количества верно предсказанных наблюдений к общему количеству наблюдений. Точность является долей наблюдений, отнесенных классификатором к положительным и являющихся истинно положительными:
Этот показатель может быть интерпретирован как измерение шума в предсказаниях классификатора, – другими словами, он показывает, с какой вероятностью наши положительные предсказания правильны.
Отметим, что высокоточные модели являются «пессимистичными» и генерируют положительные прогнозы только при полной уверенности.
Полнота – это доля наблюдений, определяемых классификатором как положительные, от всех наблюдений истинно положительного класса:
Этот показатель отражает способность модели определять наблюдения положительного класса. Модели с высоким показателем полноты являются «оптимистичными», они имеют низкую планку при генерации положительных предсказаний [5, 6].
Отметим, что показатели «точность» и «полнота» проигрывают в интуитивности показателю «правильность».
Также отметим, что если данные имеют несбалансированные классы (например, одному из классов принадлежит большая часть наблюдений), то возникает известный парадокс, когда модель обладает высокой правильностью при низкой точности предсказаний [5, 6].
F1-мера – показатель, обеспечивающий некоторый баланс между точностью и полнотой (является средним гармоническим между точностью и полнотой):
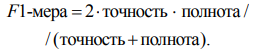
Этот показатель означает корректность полученных положительных предсказаний, он показывает, какое количество классифицированных как положительные наблюдений являются истинно положительными.
Анализируя рассмотренные показатели в совокупности, отметим, что показатель правильности
в наибольшей степени интуитивно понятен. Баланс между точностью и полнотой (компромисс между «оптимистичностью» и «пессимистичностью» модели) достигается в показателе F1-мера.
Применение метрик бинарного классификатора для оценки достоверности контроля состояния парка СТС. Опишем применение метрик на примере классической стационарной полумарковской модели эксплуатации парка СТС [1, 4]: 
где π1 – вероятность нахождения в работоспособном состоянии; π2 – вероятность нахождения в состоянии отказа; π3 – вероятность нахождения в состоянии поверки отказавшей СТС; π4 – вероятность нахождения в состоянии восстановления (ремонта); π5 – вероятность нахождения в состоянии поверки работоспособной СТС; π6 – вероятность нахождения в состоянии необнаруженного отказа; π7 – вероятность нахождения в состоянии ложного отказа; α – вероятность ложного отказа при поверке; β – вероятность необнаруженного отказа при поверке; F(T) – функция распределения отказов за время T; F(TK) – вероятность отказа на интервале времени между поверками.
В приведенных выше формулах для метрик бинарного классификатора вместо количества образцов СТС, находящихся в соответствующих технических состояниях, будем использовать вероятности нахождения в этих состояниях:
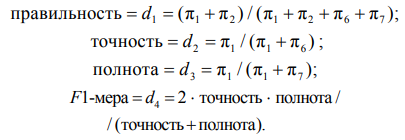
Результаты моделирования достоверности контроля технического состояния
Известно [1, 4], что существуют оптимальное значение интервала между поверками TK (ИМП)
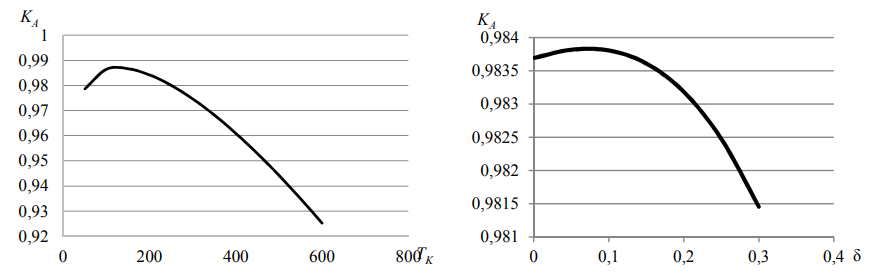
и оптимальное значение относительного допуска δ на ОП (контролируемый параметр), при которых достигается максимальное значение коэффициента готовности KA СТС к применению. На рис. 1 представлены соответствующие графики для коэффициента готовности KA для случая экспоненциального закона распределения отказов с интенсивностью λ = 0,0005.
а б
Рис. 1. Зависимости коэффициента готовности при λ = 0,0005: a – от интервала между поверками;
б – от относительного допуска на контролируемый параметр
Fig. 1. Dependencies of the readiness coefficient at λ = 0.0005: a – from period between verification;
б – from the relative tolerance for the controlled parameter
Здесь коэффициент готовности к применению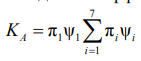 
, где ψi – средние времена нахождения СТС в соответствующих состояниях πi. На рис. 1 смоделирован процесс проведения поверки в штатной ситуации.
Зависимости показателей достоверности и коэффициента готовности от допуска на определяющий параметр при λ = 0,0005 представлены на рис. 2.
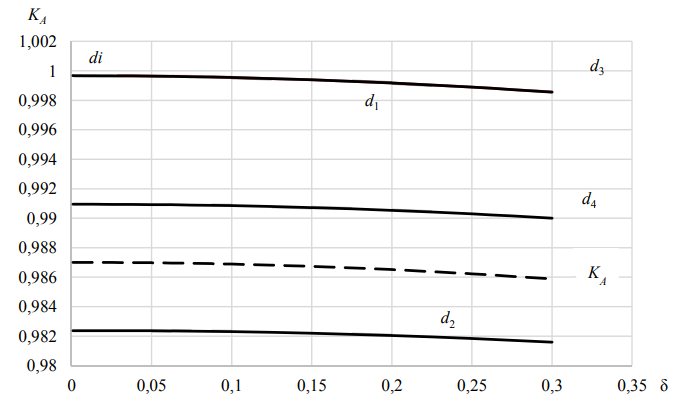
Рис. 2. Зависимости показателей достоверности и коэффициента готовности от допуска
на определяющий параметр при λ = 0,0005
Fig. 2. Dependences of reliability indicators and readiness coefficient
on the tolerance of the determining parameter at λ = 0.0005
Видно, что показатели достоверности незначительно убывают, а коэффициент готовности достигает максимума при δ = 0,1, который в масштабе графика почти не заметен. Показатели d1 и d3 практически совпадают, поскольку вероятности отказа и необнаруженного отказа – достаточно малые величины. Зависимости показателей достоверности от ИМП приведены на рис. 3.
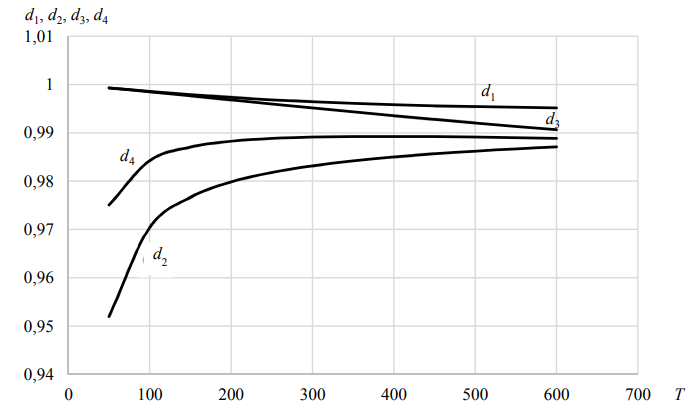
Рис. 3. Зависимости показателей достоверности от ИМП T при λ = 0,0025
Fig. 3. Dependences of reliability indicators on the PBV T at λ = 0.0025
Отметим, что показатели правильности и полноты монотонно убывают, а показатель точности и F1-мера – возрастают. Коэффициент готовности убывает от 0,857 до 0,477.
На рис. 2 и 3 моделируются внештатные ситуации, когда поверка осуществляется при различных (не оптимальных) значениях ИМП и допуска на контролируемый параметр.
Зависимости показателей достоверности от интенсивности отказов приведены на рис. 4.
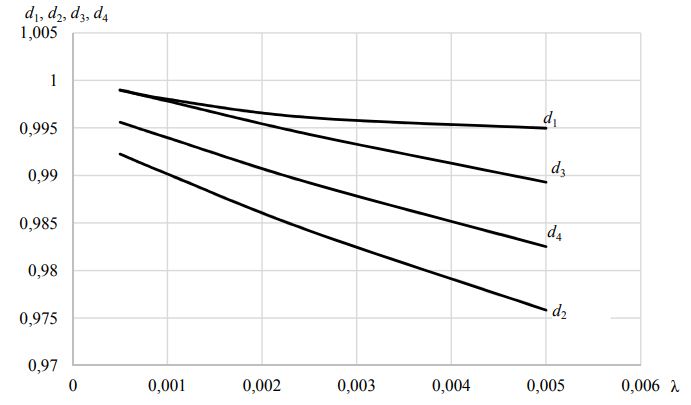
Рис. 4. Зависимости показателей достоверности от интенсивности отказов λ
Fig. 4. Dependence of reliability indicators on failure rate λ
Видно, что все показатели монотонно убывают, при этом коэффициент готовности также монотонно убывает от 0,974 до 0,445, т. е. увеличение интенсивности отказов приводит к ухудшению всех показателей достоверности. Зависимости показателей достоверности от времени восстановления (ремонта) представлены на рис. 5.
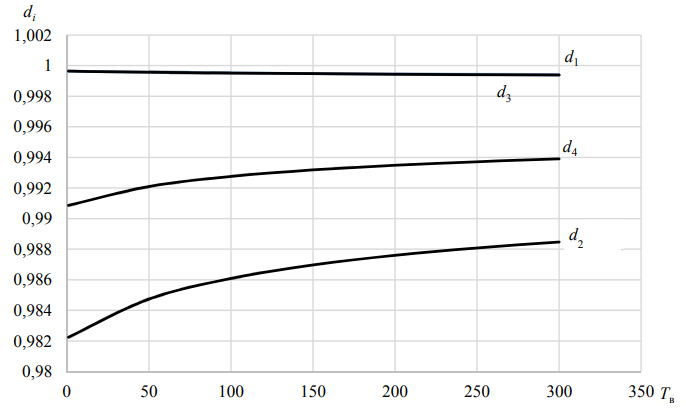
Рис. 5. Зависимости показателей достоверности от времени восстановления Tв
Fig. 5. Dependences of reliability indicators on recovery time Tв
Отметим, что показатели правильности и полноты монотонно убывают, а показатель точности и показатель F1-мера – возрастают. При этом коэффициент готовности убывает от 0,987 до 0,836. На рис. 4 и 5 моделируются внештатные ситуации, когда отказы происходят с большой интенсивностью и время восстановления (ремонта) достаточно велико.
Из представленных результатов моделирования можно сделать вывод, что наибольшее влияние на показатели достоверности и коэффициент готовности оказывают периодичность поверки и интенсивность отказов. Оператор, принимающий решение по дальнейшему управлению парком СТС в части МО, может строить прогнозы с учетом темпов изменения указанных показателей.
Обсуждения
Представленные в статье показатели достоверности применимы не только для классической модели функционирования СТС, но и для более сложных моделей, например, описанных в [8–10]. В [8, 9] рассмотрены полумарковские стационарные модели эксплуатации с двухуровневым МО, включающие два контура контроля (метрологический самоконтроль и обычную поверку), а в [10] – модель парка СТС, которая включает несколько групп деградации (риска) и по одному контуру поверки в каждой группе. Модели [8–10] имеют, как правило, по несколько одноименных основных технических состояний (например, состояние, работоспособное после поверки и после самоконтроля, состояние ложного отказа после поверки и после самоконтроля и т. д.). Для построения предложенных в статье показателей достоверности вероятности одноименных состояний в моделях [8–10] следует суммировать. Кроме рассмотренных в статье 4-х метрик бинарного классификатора в задачах бинарной классификации используются и другие метрики, например, применяется ROC-кривая, PR-кривая и т. д. [5, 6]. В задачах управления парком СТС с МО последние две метрики малоэффективны, поскольку на практике пороговые значения для ОП СТС ограничены, а для ROC- и PR-кривых пороговые значения должны меняться во всем диапазоне изменения маркеров [5, 6].
Заключение
Предложены и проанализированы показатели достоверности контроля состояний СТС с МО. На примере классической полумарковской модели эксплуатации парка СТС продемонстрированы зависимости указанных показателей от периодичности поверки, допуска на ОП, интенсивности отказов и продолжительности восстановления. Применение более широкого спектра показателей достоверности, чем традиционных метрологических показателей (вероятностей ложного и необнаруженного отказов при поверке), позволяет строить совместные оценки коэффициента готовности и достоверности контроля состояний парка СТС с МО, функционирующих в разных режимах и при разных условиях, что дает возможность оператору проектировать различные варианты стратегий управления парком СТС с МО. Полученные результаты могут быть внедрены и использованы в системе поддержки принятия решения при оперативном управлении парком СТС, в том числе при дистанционном, автоматическом или автоматизированном управлении.
1. Khayrullin R. Z., Ershov D. S., Malakhov A. V., Levina T. A. Mathematical Models of the Processes of Operation, Renewal and Degradation of a Fleet of Complex Technical Systems with Metrological Support // Axioms. 2023. V. 12 (3). P. 300.
2. Lazarenko S. V., Kostoglotov A. A., Khayrullin R. Z., Kornev A. S. Intelligent Regularized Measurement Procedure Based on the Use of a Dynamic Model of the Combined Maximum Principle and the Theory of Regularization // IOP Conference Series: Materials Science and Engineering. 2021. V. 1029 (1). P. 012083.
3. Lin T. Y., Cheng C. C. A novel opto-mechanical tol-erance analysis method for precision lens systems // Preci-sion Engineering. 2011. V. 3. P. 447–454.
4. Сычев Е. B., Храменков В. Н., Шкитин А. Д. Основы метрологии военной техники. М.: Воен. изд-во, 1993. 400 с.
5. Рассел С., Норвиг П. Искусственный интеллект. Современный подход. М.: Вильямс, 2006. 1390 с.
6. Флах П. Машинное обучение. Наука и искусство построения алгоритмов, которые извлекают знания из данных. М.: ДМК, 2015. 400 с.
7. Sukhobokov A., Belousov E., Gromozdov D., Zenger A., Popov I. A universal knowledge model and cognitive architectures for prototyping AGI // Cognitive Systems Research. 2024. V. 88. P. 101279.
8. Хайруллин Р. З., Кувыкин Ю. А., Супрунюк В. В., Смирнов А. П. Модель процесса эксплуатации измерительной системы с встроенным контролем // Тр. ВКА им. А. Ф. Можайского. 2024. Вып. 691. С. 212–218.
9. Супрунюк В. В., Кувыкин Ю. А., Щедрин А. Ю., Горбачев А. А. О метрологическом самоконтроле измерительных систем // Вестн. метролога. 2023. № 4. С. 5–9.
10. Храменков В. Н., Хайруллин Р. З. Риск-ориентированный подход при моделировании метрологического обеспечения парка средств измерений // Измерительная техника. 2023. № 11. C. 10–16.
