Россия
Комбинаторная оптимизация на сегодняшний день получила повсеместное распространение в науке, промышленности и экспертной среде. Решения о распределении ресурсов, разработке экспериментов, планировании задач или выборе наиболее эффективного пути зачастую приходится выбирать из множества вариантов. И в данном классе задач методы комбинаторной оптимизации обладают значительным потенциалом, поскольку могут помочь находить оптимальные или близкие к оптимальным варианты, способствуя принятию более взвешенных и рациональных решений. Изучены вопросы, связанные с применением методов комбинаторной оптимизации для проектирования процессов производства при ограниченных ресурсах. В процессе исследования описан подход проектирования, который учитывает потребности конкретного производственного процесса, наличие ресурсов, объем их использования и последовательность. Отдельное внимание уделено выбору и обоснованию целевой функции. С учетом полученных результатов формализован алгоритм комбинаторной оптимизации, реализуемый на базе нейронной сети HyperGNN. Предложенный алгоритм апробирован на примере производственной цепочки машиностроительного предприятия. В ходе апробации рассматривались реальные, четко определенные ресурсы: фрезерный станок, сварочный аппарат, шлифовка, термообработка и монтаж. Все задачи имели конкретную длительность, логическую последовательность и фиксированные требования. Полученные данные демонстрируют высокую прикладную значимость разработанного алгоритма. В ходе его сравнительного анализа с методом жадного распределения ресурсов установлено, что предложенный подход существенно превосходит традиционные методы планирования по ряду ключевых критериев, включая снижение общего времени выполнения производственного цикла, уменьшение количества конфликтов за ресурсы, более равномерную загрузку оборудования и сокращение простоев между операциями.
оптимизация, ресурсы, нейронная сеть, ограничения, производство, алгоритм
Введение
Комбинаторная оптимизация (КО) – это подкласс задач оптимизации, который находит свое применение практически повсеместно в сценариях распределения ресурсов, планирования и маршрутизации во многих областях и сферах деятельности. Например, транспортные компании используют КО с целью выбора наиболее эффективных графиков и маршрутов доставки. При этом учитываются такие основополагающие факторы, как дорожные условия, местоположение пункта назначения, временные окна. Включение данных детерминант в контур моделирования и решения позволяет сократить время в пути и расход топлива, а также повысить удовлетворенность клиентов, обеспечив своевременную и эффективную доставку продукции [1]. Предприятия машиностроения применяют КО для эффективного распределения ограниченных ресурсов, к которым относится станочный парк с различными типами оборудования, квалифицированный персонал, а также доступное время. Целью при этом часто является минимизация общего времени выполнения заказа, снижение производственных издержек или максимизация объема выпускаемой продукции.
Универсальность модели КО и ее популярность объясняется тем, что во многих практических приложениях деятельность и ресурсы, такие как оборудование, автомобили, занятый персонал, являются неделимыми. Кроме того, многие задачи (например, составление расписания) имеют правила, четко определяющие конечное число допустимых вариантов, и, следовательно, они могут быть сформулированы с помощью процедур, преобразующих логические описания альтернатив в линейные описания ограничений, в которых некоторое подмножество переменных должно принимать определенные дискретные значения. При этом следует отметить, что, хотя дискретный характер оптимизационных задач позволяет решать их за конечное время путем поочередного перечисления решений-кандидатов и выбора оптимального варианта, число таких кандидатов быстро растет с размером входных данных, что делает многие прикладные задачи оптимизации неразрешимыми для простых схем перечисления.
Исследователи КО выявляют структурные особенности задач оптимизации и используют их для разработки как точных, так и приближенных общих методов решения. Обычно эти проблемы КО классифицируются по их вычислительной сложности [2].
Итак, задача КО заключается в поиске и нахождении максимума или минимума объективной функции в дискретной области, а не в непрерывном пространстве. Другими словами, c точки зрения математики задача КO заключается в поиске оптимальной комбинации элементов из некоторого набора объектов, в котором решение либо является дискретным множеством, либо может быть упрощено до дискретного множества. В целом проблема КО артикулируется в качестве достижения минимизации или максимизации, в зависимости от конкретных сценариев заданных целевых функций. В алгоритмическом плане задачи максимизации и минимизации рассматриваются эквивалентно, с учетом одной и той же вычислительной логики.
Общие математические структуры, используемые в КО, включают в себя:
1. Матроиды: они необходимы для обобщения концепции линейной независимости в векторных пространствах и моделирования комбинаторных задач с определенными ограничениями.
2. Графы: находят свое применение в процессе моделирования сетей, где объекты являются вершинами, а ребра – отношениями или связями между ними.
3. Полиэдры: геометрические представления областей выполнимости в линейном программировании, где решения находятся в вершинах [3].
Особую значимость КО приобретает в задачах оптимизации распределения ресурсов для проектирования производственных процессов, поскольку они являются одними из самых сложных объектов в управлении современными предприятиями. Эта комбинаторная проблема имеет сразу несколько целей (распределение с ограниченными ресурсами, ограничение продолжительности производственного цикла, необходимость выравнивания ресурсов). Кроме того, ее размер и сложность растут экспоненциально по мере увеличения количества действий, типов ресурсов и режимов выполнения производственных задач [4].
С учетом отмеченного тематика данной статьи является теоретически и практически значимой.
Анализ публикаций по теме исследования
Над разработкой методов оптимизации, путем изучения эвристики или ключевых политик в алгоритмах КО, с тем чтобы эти методы были способны достигать высококачественных результатов, трудятся С. Ю. Ветров [5], М. В. Сарамуд, Е. А. Спирин, Е. П. Талай, Я. Ю. Пикалов [6], Kim Hyeongwook, Kim Miseong, Lee Aejin, Park Hea-Lim [7].
Способы решения проблемы выбора группы производственных ресурсов для предоставления услуг по заказу с учетом множества целей, таких как минимальная стоимость, кратчайший производственный цикл и максимальная скорость доставки, на базе КО разрабатывают Д. Н. Шмыглёв, В. А. Судаков [8], Д. М. Лысанов, И. И. Еремина, А. Э. Шайхатаров [9], Jannis Rose, Patrick Forman, David Stieler, Achim Menges, Peter Mark [10].
Исследования, направленные на переформулирование задач КО, которые допускают их разрешимость с помощью современных вычислительных технологий, входят в круг научных интересов Д. Р. Стахина, Д. Г. Плотникова, М. Г. Соломатова [11], А. В. Дятчиной, С. А. Олейниковой, Т. Н. Недиковой [12], Hui-Min Li, Jin-Min Liang, Zhi-Xi Wang, Shao-Ming Fei [13].
Нерешенные части общей проблемы
Высоко оценивая имеющиеся на сегодняшний день труды и наработки, следует акцентировать внимание на том, что еще достаточно широкий спектр вопросов требует более углубленного исследования. Так, например, особого внимания заслуживают перспективы использования гиперграфовых нейронных сетей, которые могут стать ценным инструментом для решения задач КО с ограничениями более высокого порядка. Кроме того, не в полной мере проработанными остаются проблемы попадания в ловушку субоптимальных локальных решений и проблемы масштабируемости, которые характерны для подходов к решению задач КО, основанных на обучении без наблюдения.
Таким образом, цель статьи заключается в рассмотрении особенностей применения методов КО для проектирования процессов производства при ограниченных ресурсах.
Описание процесса планирования производства
Требуемые работы, отношения приоритета, длительность работ и обычные потребности в ресурсах для каждого процесса приведены в табл. 1.
Таблица 1
Table 1
Данные для планирования производства
Data for production planning
|
Основной процесс |
Предыдущий процесс |
Продолжительность, мин |
Ресурс |
|
1.1 |
– |
5 |
А |
|
1.2 |
1.1 |
2 |
Б |
|
1.3 |
1.2 |
7 |
Г |
|
1.4 |
1.3 |
12 |
В |
|
1.5 |
1.4 |
4 |
Д |
|
1.6 |
1.5 |
2 |
Б |
|
1.7 |
1.6 |
7 |
А |
|
1.8 |
1.7 |
9 |
Д |
На рис. 1 представлена сетевая диаграмма процесса планирования, которая является эффективным и упорядоченным инструментом КО, обеспечивающим четкий визуальный взгляд в логической форме на взаимосвязь между различными процессами и необходимыми ресурсами.
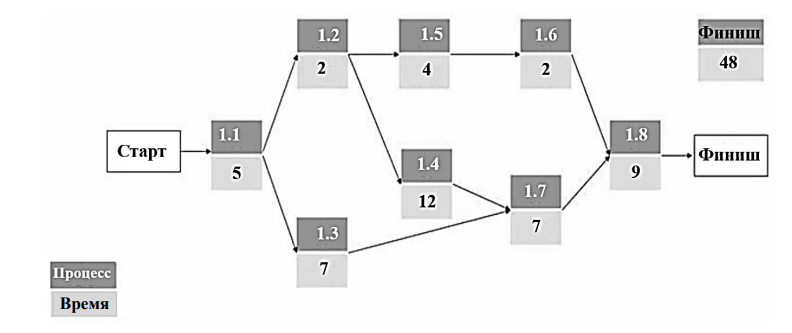
Рис. 1. Сетевая диаграмма процесса производственного планирования
Fig. 1. Network diagram of the production planning process
Далее представляется целесообразным ввести в решение задачи глобальные ограничения, которые отражают повторяющиеся подструктуры моделирования, включающие множество переменных. Помимо удобства в ходе моделирования, глобальные ограничения необходимы для обоснования наиболее эффективного решения, поскольку они реализуются специальными алгоритмами распространения, которые еще больше сокращают пространство поиска [14]. Учитывая поставленную цель моделирования, предлагаем использовать следующие три глобальных ограничения:
1. Кумулятивное 
гарантирует, что набор из n производственных процессов не превысит заданную емкость ресурса b, где каждая задача процесса i определяется временем начала s(i), продолжительностью d(i) и потребленными единицами ресурса c(i):
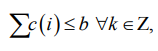
где k – индекс текущего рассматриваемого ресурса (обычно номер ресурса, если ресурсов несколько); b – максимальная емкость ресурса, которую нельзя превышать одновременно всеми операциями (заданная величина ресурса); Z – упорядоченный список пар вида (s(i), d(i), c(i)), где s(i) – время старта операции i; d(i) – продолжительность операции i; c(i) – объем потребления ресурса процессом i (сколько единиц ресурса нужно для выполнения задачи i).
2. Без перекрытия 
– гарантирует, что набор из n производственных процессов не перекрывается, где каждая задача i определяется ее началом l(i), окончанием r(i), ожиданием завершения предыдущей задачи t(i) и ожидаемым эффектом b(i):
где j – индекс текущей задачи/операции (номер операции); L – список интервалов (задачи характеризуются временными рамками и ожиданиями завершения предыдущих операций), содержащий кортежи вида (l(i), r(i), t(i), b(i)), где l(i) – начало интервала задачи i, r(i) – конец интервала задачи i, t(i) – минимальное время ожидания завершения предыдущей задачи перед запуском следующей, b(i) – ожидаемый эффект или выгода от выполнения задачи i.
3. Элемент (x, a, y) обобщает доступ к массивам переменных, гарантируя, что переменная y равна
x-му элементу массива a целых чисел или целочисленных переменных:
a[x] = y.
Данное ограничение можно распространить на многомерные массивы при условии, что для индексации используется только одна целочисленная переменная [15]. Ограничения, использующие функции поиска, такие как f(x) = y, могут быть выражены как f [x] = y путем преобразования f в массив. На основании этого также можно реализовать следующее ограничение:
y ∈ a[x],
введя для каждого такого ограничения новый массив b целочисленных переменных, где каждая целочисленная переменная b[i] имеет область, равную a[i], и обеспечив выполнение b[x] = y.
Обоснование целевой функции
Неотъемлемым элементом проектирования процессов производства при ограниченных ресурсах является выбор целевой функции либо установление справедливости в КО. В рамках поставленной задачи есть множество W производственных процессов и множество T ресурсов, которые необходимы для их реализации. Очевидно, что если w-процесс предполагает решение набора 
задач, то возникают затраты cw(S). Если все задачи из S не могут быть выполнены в рамках процесса w, то cw(S) равно бесконечности. Таким образом, необходимо найти такое распределение ресурсов между производственными процессами, которое минимизирует общую стоимость.
Иными словами, необходимо решить:
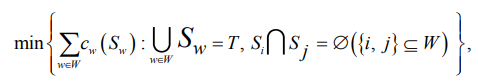
где Sw – набор заданий, которые должны быть выполнены в рамках производственного процесса w; w – частный случай индексации элементов множества производственных процессов W, используется как переменная суммирования, когда рассматривается общий вклад каждого отдельного процесса
в итоговую величину (например, суммарная нагрузка); 
(«пустое множество») – специальный символ математики, означающий отсутствие каких-либо элементов (например, условие Si ∩ Sj = 
Si ∩ Sj = 
означает, что наборы заданий различных процессов не пересекаются друг с другом); cw(Sw) – функция производственной нагрузки процесса w, зависящая от набора заданий Sw, она отражает стоимость или объем работ, связанных
с выполнением данного набора задач.
Пусть cw(Sw) будет «производственной нагрузкой» процесса w. Если в данном реализуемом решении один процесс имеет значительно меньшую производственную нагрузку, но потребляет большее количество ресурсов, то такой вариант распределения не является оптимальным. Для решения этой проблемы можно воспользоваться следующими способами:
– минимизировать максимальную нагрузку на наиболее ресурсоемкий процесс;
– минимизировать выпуклую комбинацию средней и максимальной нагрузок;
– минимизировать сумму k наибольших нагрузок;
– минимизировать максимальную нагрузку, затем вторую по величине и т. д. в лексикографическом порядке;
– минимизировать выпуклую комбинацию средней рабочей нагрузки и разницы между максимальной и минимальной нагрузками;
– наложить верхнюю границу на рабочие нагрузки;
– накладывать как нижние, так и верхние ограничения на рабочие нагрузки;
– минимизировать сумму квадратов нагрузок;
– минимизировать 
– норму вектора рабочей нагрузки для некоторого p > 1, т. е. количество:
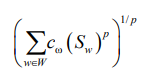
Таким образом, принимая во внимание вышеизложенное, можно отметить, что решение поставленной задачи предполагает многоцелевую оптимизацию.
Подход к решению задачи многоцелевой оптимизации
Экземпляр π задачи многоцелевой оптимизации Π задается набором из m функций f1, ..., fm. Каждая fi: X → R+ определена на одном и том же множестве выполнимых решений X. Пусть |π| обозначает размер двоичного кодирования экземпляра π. Предположим, что каждая fi принимает значения
в диапазоне 
для некоторого полинома p. Далее необходимо определить Парето-оптимальную границу для многообъектных задач минимизации. Парето-оптимальная граница, обозначаемая P(π), – это множество решений x ∈ X, такое, что не существует x' ∈ X, такого, что 
для всех i, со строгим неравенством хотя бы для одного i. Другими словами, P(π) состоит из всех недоминируемых решений.
Сформулированная оптимизационная задача может быть решена непосредственно с помощью методов градиентного спуска, с последующим преобразованием непрерывных результатов в дискретные значения [16]. Методы, основанные на штрафах, также являются обычной практикой в этих подходах, чтобы гарантировать, что ограничения будут удовлетворены в конечном результате [17]. Однако можно добиться лучших решений, решив альтернативную задачу оптимизации. В этой альтернативной задаче оптимизации переменные pi представляют собой результаты функции преобразования на основе HyperGNNs. Такие функции преобразования используются с целью уловить сложные закономерности и взаимозависимость переменных через ограничения задачи и, следовательно, получить лучшие решения [18].
В данном случае речь идет о параметризованной функции преобразования, основанной на HyperGNNs. В частности, предлагаем рассматривать p = G(σ; W) или pi = Gi(σ; W) для i ∈ N, где pi – это (непрерывное) назначение узла i, W – вектор параметров функции преобразования G на основе HyperGNN, а σ = [σ1, …, σN] – это входное вложение (σi – входное вложение узла i). Используя параметризованную функцию преобразования, можно оптимизировать цель, одновременно используя качественную функцию преобразования (W) и оптимизируя входное вложение (σ).
Алгоритм решения задачи КО в процессе проектирования процессов производства при ограниченных ресурсах с использованием нейронной сети HyperGNN представлен на рис. 2.
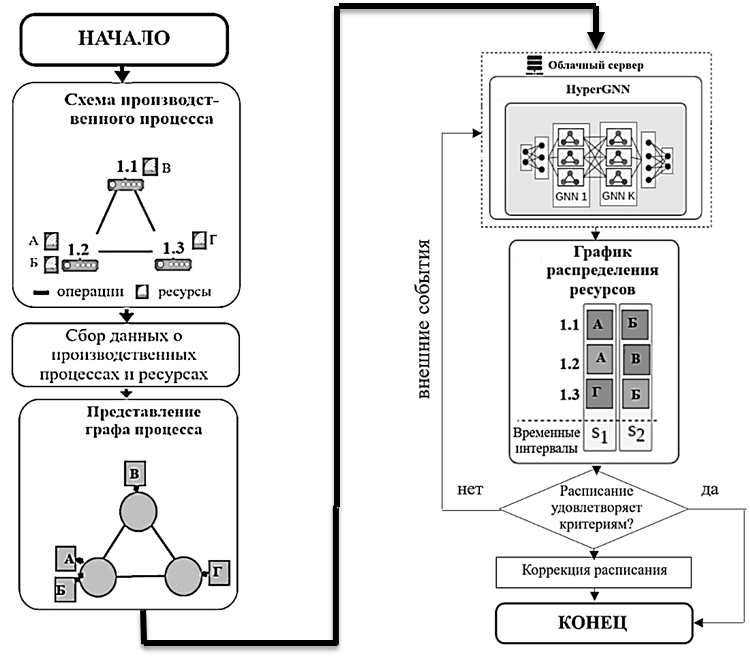
Рис. 2. Алгоритм решения задачи комбинаторной оптимизации при распределении ресурсов
Fig. 2. An algorithm for solving the combinatorial optimization problem in resource allocation
Согласно рис. 2 HyperGNN генерирует расписание распределения ресурсов с помощью модели машинного обучения на основе трансформатора GNN.
Шаг 1: сбор информации о потребностях производственных процессов, их последовательности и требуемых ресурсах.
Шаг 2: оценка наличия имеющихся ресурсов, их достаточности, комплектности, возможности использования.
Шаг 3: построение графового представления производственного процесса.
Шаг 4: генерирование расписания распределения ресурсов путем итеративной классификации узлов.
Шаг 4: оценка расписания.
Шаг 5: принятие решения. Если расписание удовлетворяет требованиям, оно распространяется на все точки поставки ресурсов и добавляется к обычному расписанию работы производства. Алгоритм завершен.
Если обнаружены изменения в результате действия внешних событий (поломка, срочный заказ, отмена), то осуществляется возврат к шагу 3 → пересбор графа → коррекция расписания.
Апробация предложенного подхода к решению задачи многоцелевой оптимизации
Для апробации предложенного на рис. 2 алгоритма рассмотрим производственный процесс из табл. 1 применительно к машиностроительному предприятию.
Согласно табл. 1 в производственном процессе машиностроительного предприятия задействованы следующие ресурсы:
– ресурс А – универсальный обрабатывающий центр (например, фрезерный станок);
– ресурс Б – сварочная станция (2 операции);
– ресурс В – участок термообработки;
– ресурс Г – станок шлифовки;
– ресурс Д – монтажный стенд (2 операции).
Все ресурсы являются ограниченными – каждый тип ресурса доступен только в одном экземпляре (ресурсы неделимы и невозобновляемы в течение производственного дня). Это создает типичный сценарий конфликта при наивном планировании (например, два процесса требуют ресурс Б
в разное время, но интервал между ними слишком мал, и возникает накладка).
Для проведения расчетов рассмотрим два подхода:
1. Базовый метод (BAS): традиционное жадное распределение ресурсов без оптимизации (по мере поступления задач).
2. Предложенный метод (HYP): алгоритм HyperGNN, учитывающий глобальные ограничения, логическую последовательность и минимизацию суммарной нагрузки.
В табл. 2 представлены результаты проведенных расчетов.
Таблица 2
Table 2
Результаты апробации различных подходов к решению задачи многоцелевой оптимизации
The results of testing various approaches to solving the problem of multi-purpose optimization
|
Метрика |
Метод |
Улучшение, |
|
|
BAS |
HYP |
||
|
Общее время выполнения задания, мин |
48 |
40 |
16,7 |
|
Количество конфликтов ресурсов, количество случаев |
3 |
0 |
100 |
|
Нагрузка самого загруженного ресурса, мин |
16 |
12 |
25 |
|
Количество простоев между задачами, количество временных промежутков |
5 |
2 |
60 |
|
Количество переназначений ресурсов, количество случаев |
4 |
1 |
75 |
|
Функция стоимости распределения, у. е. |
136 |
102 |
25 |
Анализируя данные, приведенные в табл. 2, можно отметить следующее. С точки зрения общего времени выполнения задания, которое оценивает продолжительность всего производственного цикла, HyperGNN показал меньшую длительность за счет рационального выравнивания ресурсоемких процессов. Также предложенный алгоритм позволил решить проблему с конфликтом ресурсов. В базовом методе наблюдаются одновременные запросы на один и тот же ресурс, что исключается в HyperGNN через ограничение «без перекрытия». Что касается нагрузки, которая отражает максимальную занятость любого одного ресурса, то использование HyperGNN позволило более равномерно ее распределять.
Итак, предложенный алгоритм HyperGNN доказал эффективность по следующим показателям:
1. Снижение общего времени производства на 16,7 % означает, что предприятие может быстрее выполнять заказы, повышая при этом производительность.
2. Устранение конфликтов ресурсов доказывает, что глобальные ограничения реализованы корректно.
3. Улучшение равномерности загрузки ресурсов уменьшает износ оборудования и риск сбоев.
4. Снижение суммарной стоимости распределения на 25 % свидетельствует о реальном экономическом эффекте.
5. Меньшее количество переназначений и простоев повышает стабильность производственного процесса в целом.
Заключение
Описан подход к использованию методов комбинаторной оптимизации для проектирования процессов производства при ограниченных ресурсах, который учитывает потребности конкретного технологического процесса, наличие ресурсов, объем и последовательность их использования.
Оптимизация направлена на минимизацию общих затрат, связанных с перераспределением ресурсов, превышением сроков их использования и предотвращением накладок. В рамках предложенного подхода формализован алгоритм решения задачи КО с использованием нейронной сети HyperGNN. Предложенный алгоритм апробирован на примере производственного процесса машиностроительного предприятия. Полученные результаты подтверждают его высокую эффективность в решении задач комбинаторной оптимизации распределения ресурсов. Он превосходит традиционные методы по ключевым метрикам. В реальных условиях внедрение данного алгоритма может привести к снижению производственных издержек, сокращению времени выполнения заказов и повышению устойчивости производственного цикла предприятия.
1. Семенкина О. Е., Становов В. В., Попов Е. А. Иерархический самоконфигурируемый алгоритм кооперативной коэволюции для решения задачи составления расписания // Вестн. Москов. гос. техн. ун-та им. Н. Э. Баумана. Сер.: Приборостроение. 2023. № 4 (145). С. 131–148.
2. Cong Zhang, Yaoxin Wu. A review on learning to solve combinatorial optimisation problems in manufacturing // IET Collaborative Intelligent Manufacturing. 2023. V. 5. Iss. 1. Р. 99–107.
3. Xu Guo, Xiaoyu Song. A synergic quantum particle swarm optimisation for constrained combinatorial test generation // IET Software. 2022. V. 16. Iss. 3. Р. 120–129.
4. Сохраби М., Фатхоллахи-Фард А. М., Громов В. А. Алгоритм генетической инженерии (GEA): эффективный метаэвристический алгоритм для решения задач комбинаторной оптимизации // Автоматика и телемеханика. 2024. № 3. С. 23–37.
5. Ветров С. Ю. Оптимизация планирования партии изделий в условиях ограниченных производственных ресурсов // Междунар. журн. информац. технологий и энергоэффективности. 2025. Т. 10. № 4 (54). С. 154–159.
6. Сарамуд М. В., Спирин Е. А., Талай Е. П., Пикалов Я. Ю. Оптимизация организации технологических процессов в условиях облачного производства // Математические методы в технологиях и технике. 2022. № 12. С. 235–240.
7. Hyeongwook Kim, Miseong Kim, Aejin Lee, Hea-Lim Park. Organic Memristor-Based Flexible Neural Net-works with Bio-Realistic Synaptic Plasticity for Complex Combinatorial Optimization // Advanced Science. 2023. V. 10. Iss. 19. P. 12–19.
8. Шмыглёв Д. Н., Судаков В. А. Модель обучения с подкреплением для оптимизации автопарка предприятия // Препринты ИПМ им. М. В. Келдыша. 2024. № 39. С. 1–13.
9. Лысанов Д. М., Еремина И. И., Шайхатаров А. Э. Разработка математической модели рационального распределения задач между исполнителями // Экономика и предпринимательство. 2025. № 4. С. 1164–1167.
10. Rose J., Forman P., Stieler D., Menges A., Mark P. Combinatorial optimization approach for the efficient reuse of RC components // Structural Concrete. 2025. N. 56. Р. 189–195.
11. Стахин Д. Р., Плотников Д. Г., Соломатов М. Г. Управление рисками эксплуатации подъемно-транспортного оборудования на основе решения np-полной задачи комбинаторной оптимизации // Транс-портное, горное и строительное машиностроение: наука и производство. 2024. № 26. С. 47–53.
12. Дятчина А. В., Олейникова С. А., Недикова Т. Н. Разработка проблемно-ориентированной системы для решения оптимизационной задачи управления потоком поступающих заявок // Вестн. Воронеж. гос. техн. ун-та. 2023. Т. 19. № 4. С. 37–43.
13. Hui-Min Li, Jin-Min Liang, Zhi-Xi Wang, Shao-Ming Fei. Ising Hamiltonians for Constrained Combinatorial Optimization Problems and the Metropolis-Hastings Warm-Starting Algorithm // Advanced Quantum Technologies. 2025. V. 6. Iss. 9. P. 45–53.
14. Жуков В. П. Моделирование и оптимизация регулярных многоступенчатых многопродуктовых гравитационных классификаторов // Вестн. Иванов. гос. энергет. ун-та. 2023. № 4. С. 77–84.
15. Zhongfei Zhang, Ting Qu. Digital twin-based pro-duction logistics resource optimisation configuration method in smart cloud manufacturing environment // IET Collaborative Intelligent Manufacturing. 2024. V. 6. Iss. 4. Р. 56–62.
16. Jingjing Zhao, Fan Zhang. Agent-based simulation system for optimising resource allocation in production process // IET Collaborative Intelligent Manufacturing. 2025. V. 7. Iss. 1. Р. 120–129.
17. Зотов С. А. Использование «задачи рюкзака» – комбинаторной оптимизации ресурсов бизнес-процессов для предприятия горнодобывающей отрасли // Инновации и инвестиции. 2024. № 5. С. 477–480.
18. Ruizhao Zheng. Multi-objective particle swarm op-timisation of complex product change plan considering service performance // CAAI Transactions on Intelligence Technology. 2023. V. 8. Iss. 3. Р. 61–65.
