When operating vessels in stormy conditions, the problem of flooding arises, an extreme case of which is the burying of the bow end in a wave. In this case, hydrodynamic loads of significant magnitude may act on the deck at the bow end and above-deck structures, which may result in a violation of local and general strength, as well as the loss of the vessel due to the loss of stability. The magnitude of these loads can be estimated based on modeling the longitudinal roll of the vessel, taking into account the burying of the bow end of the vessel in a wave. Using the complete system of equations of longitudinal roll, a mathematical model was proposed that allows describing the dynamics of a vessel in head waves under conditions of periodic burying of the bow end in a wave. This model can be used to calculate the hydrodynamic loads acting on the deck when the bow end buries in a wave. An assessment was made of the effect of changes in added masses and moments of inertia on the dynamics of the vessel and the magnitude of the loads. The results obtained using the proposed model are compared with those obtained within the framework of a simplified scheme that does not take into account the effect of vertical rolling on pitching. The results of the comparative analysis showed the possibility of using both approaches to assess the magnitude of hydrodynamic loads. Using the proposed model, an assessment of bending moments at the midship under irregular waves was performed.
heave, pitch, hydrodynamic loading, bow burying, loss of stability, bending moment, irregular waves
Введение
Эксплуатация судов в штормовых условиях нередко сопровождается заливанием палубы, а при большой высоте волн и амплитуде вертикальной качки может происходить зарывание носовой оконечности в волну. При этом возникают гидродинамические нагрузки, приводящие к возникновению повреждений палубы и надпалубных конструкций [1, 2], а также к потере общей прочности корпуса [3, 4]. Кроме того, под действием гидродинамической нагрузки, приложенной к палубе судна, происходит падение поперечной метацентрической высоты и трансформация диаграммы статической остойчивости, что в совокупности с кренящим моментом, вызванным несимметричностью обтекания, может привести к опрокидыванию судна [5]. Поэтому необходимо располагать методами моделирования динамики судов в условиях заливания носовой оконечности и ее зарывания в волну.
Подходы к моделированию заливаемости
Традиционно при моделировании динамики судна на встречном волнении используется система дифференциальных уравнений вертикальной и килевой качки. Решение данной системы позволяет определить параметры качки судна, а также оценить возможность попадания воды на палубу путем построения кривых заливаемости [6].
Для изучения явления заливаемости широко применяются экспериментальные методы. Так, в ра-боте [7] отмечены многочисленные серьезные повреждения судовых конструкций в штормовых условиях, таких как проваливание палуб бака и верхней палубы в носовой оконечности, выпучивание опор между палубами, падение крышек люков в трюмы, обрушение передних стенок мостика и т. д. Отмечается, что существует много неясностей в задачах определения пиковых давлений ударов волн, их продолжительности, механизмов генерации и упругопластических реакций всей конструкции судна и ее отдельных элементов.
Авторами были проведены экспериментальные исследования, в рамках которых осуществлялась буксировка модели судна из дерева на различных скоростях в условиях регулярного волнения различной высоты и длины в экспериментальном бассейне. В процессе испытаний фиксировалась высота волны в носу, параметры килевой и вертикальной качки, ударные давления волн на палубу, продольные изгибающие моменты и параметры волновой вибрации. Определено, что гидродинамические воздействия волн на палубу при сильном волнении проявляются в виде падения нагромождений брызг и набегания волн, а также в условиях зарывания в волну при сильной качке.
Установлено, что максимальное ударное давление для палубы бака может достигать величины 50 т/м2 в самых тяжелых условиях. Также отмечено, что напряжения от вибрационного изгибающего момента из-за ударов волн могут достигать величины 40~70 % от вызванных волновым изгибающим моментом в условиях движения на регулярном волнении.
В статье [8] приводятся результаты численного моделирования явления заливаемости на примере контейнеровоза S-175 на регулярном волнении с использованием собственного решателя naoe-FOAM-SJTU. Показано, что характер движения судна демонстрирует сильную нелинейность. Авторы отмечают, что для килевой качки положительная амплитуда и отрицательные амплитуды имеют разную величину, что объясняется нелинейным характером изменения восстанавливающей силы. Показана возможность применения данного подхода для изучения явления динамики судна в условиях заливаемости. При этом анализ нагрузок, действующих на палубу и надпалубные конструкции, в статье не выполнялся.
В статье [9] представлена возможность повреждений палуб морских платформ и судов вследствие их заливания в условиях сильного волнения. Авторами выполнено исследование данного явления с использованием метода гидродинамики сглаженных частиц (SPH). В рамках проведенного вычислительного эксперимента положение горизонтальной палубы над средним уровнем воды было фиксированными. Отмечено сильное изменение кинематики волны и выполнена оценка величин гидродинамических нагрузок, действующих на палубу.
В работе [10] описан метод численного моделирования волновой нагрузки в условиях заливания палубы судна. Для моделирования явлений на границе раздела сред использовался модифицированный метод объема жидкости (VOF), относящийся к Эйлеровым методам. Результаты моделирования заливания сопоставлены с результатами модельных испытаний. Отмечено, что расчетное количество воды на палубе несколько больше, чем в модельном тесте, а давление на конструкцию палубы сопоставляется хорошо. Пиковые значения давлений на палубу, полученные в данной работе, достигают 4·105 Па, что согласуется с данными работы [7].
В работе [11] отмечается, что заливание палубы судна является высокодинамичным процессом, сопровождающимся значительной деформацией свободной поверхности жидкости, что обусловливает целесообразность применения метода SPH для решения данной задачи. В этой статье SPH использовался для прогнозирования поведения жидкости при исследовании взаимодействия между судном (представленным твердым телом) и бегущими волнами. Прогнозируемые высоты воды на палубе сравнивались с экспериментальными результатами.
Отмечено, что в случае двумерной постановки задачи SPH обеспечивает надежный прогноз периода затопления водой и пиковых значений уровня воды. В трехмерном случае возникла необходимость реализации ряда мероприятий, направленных на снижение затрат вычислительных мощностей. В частности, пришлось уменьшить разрешение по сравнению с использованным для двумерного анализа, а также разделить вычислительную область специальным образом установленными границами, на которые налагались определенные условия, взятые из решения, полученного с использованием сеточных методов.
Кривая для прогнозируемой высоты воды на палубе в случае трехмерной модели имеет множество скачков, что вызвано относительно низким разрешением. Однако, как отмечают исследователи, в целом SPH обеспечивает приемлемое прогнозирование высоты воды на палубе, а с увеличением разрешения ожидается его улучшение.
Большой объем повреждений палубных механизмов и конструкций надстройки наблюдался на судах типа FPSO (плавучая установка для добычи, хранения и отгрузки нефти) в результате заливания палубы [12]. В работе отмечается, что линейный дифракционный анализ с эмпирическими поправками дает приемлемые результаты, но ни один метод расчета или программа не способны проанализировать это явление в полной мере. Авторы указывают на необходимость проведения модельных испытаний для прогнозирования заливания палубы и величины гидродинамических нагрузок. Представлены оценки пиковых значений гидродинамических нагрузок на конструкции надстройки, которые составляют порядка 180 кПа.
Установлено, что максимальную заливаемость вызывает необязательно самая большая волна. Процесс происходит так, что на судно воздействуют одна или несколько волн, раскачивающих его, а за ними следует относительно большая волна. По мнению исследователей, это является наиболее критическим условием для явления заливаемости. При этом максимальная сила удара, например по надстройке или оборудованию в носовой части, необязательно происходит на той же волне, что вызывает максимальное заливание в носовой части.
Влияние формы носовой оконечности на возникновение заливаемости было темой обсуждения на протяжении многих лет [13, 14]. В работах отмечается, что заливаемость палубы и сопутствующие гидродинамические нагрузки сильно зависят от высоты борта в носу и скорости движения судна. При этом форма носа незначительно влияет на процесс заливания палубы.
Другие авторы [15] приходят к выводу о том, что форма носовой оконечности влияет на процесс заливаемости, но никаких четких тенденций в результате модельных испытаний не выявлено. В большинстве работ отмечается положительный эффект за счет увеличения надводного борта.
На основании упрощенного метода расчета продольной качки [16], предложенного А. В. Герасимовым, В. А. Мореншильдт и Ю. А. Нецветаевым в [3, 4], была разработана математическая модель, позволяющая изучать поведение судна в условиях зарывания в волну носовой оконечности и оценивать величины гидродинамических нагрузок, действующих на палубу в носовой оконечности. Величина указанных нагрузок вычисляется из условия обтекания носовой оконечности потоком жидкости, причем скорость обтекания определяется характером движения носовой оконечности и волновых частиц. К основным допущениям метода [16] относится пренебрежение влиянием вертикальной качки на килевую, а также предположение о симметричности обводов судна относительно мидель-шпангоута.
Повышение производительности ЭВМ способствовало тому, что при решении подобных задач стали широко применяться методы вычислительной гидродинамики и, в частности, метод гидродинамики сглаженных частиц [17, 18]. Однако использование подобных методов требует затрат больших вычислительных мощностей, что в некоторых случаях может оказаться проблематичным. Такая ситуация имеет место, например, при реализации процедур контроля прочности и остойчивости в бортовых интеллектуальных системах поддержки принятия решения, когда время на выработку рекомендаций судоводителю ограничено [19]. При этом моделирование динамики судов на встречном волнении с ис-пользованием традиционных подходов позволяет существенно сократить время на получение решения, а потому не утратило актуальности и сегодня.
В настоящей статье представлена математическая модель для оценки динамики судна на встречном волнении в условиях зарываемости носовой оконечности, построенная на основе полной системы дифференциальных уравнений продольной качки [20], в которой удерживаются все члены, в отличие от модели [16].
Разработка математической модели
Для определения гидродинамических воздействий на палубу судна в носовой оконечности в условиях зарываемости воспользуемся представленной в [20] системой уравнений продольной качки судна:
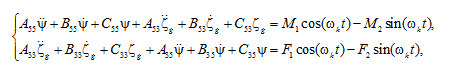
(1)
где А33, А55, А53, А35 – коэффициенты инерционных сил; В33, В55, В53, В35 – коэффициенты демпфирующих сил; С33, С55, С53, С35 – коэффициенты восстанавливающих сил; M1, M2, F1, F2 – составляющие возмущающих сил; ωk – кажущаяся частота волны, с–1; t – время; ψ – угол дифферента судна, рад; ζg – аппликата центра тяжести судна, м.
Коэффициенты в (1) вычисляются в связанной с судном системе координат Gx'y'z' по методу плоских сечений согласно [20]:
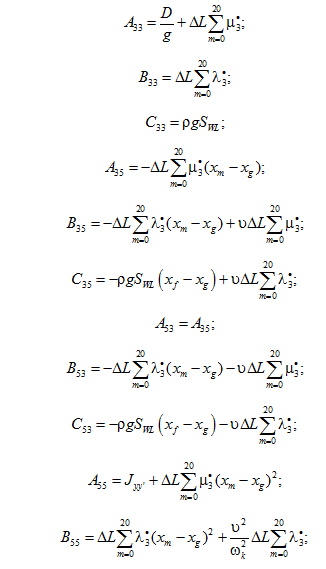
где D – весовое водоизмещение судна, кН; ΔL – теоретическая шпация, м; 
– присоединенная масса на единицу длины судна, т/м; 
– коэффициент демпфирования на единицу длины судна, (кН·с)/м2; xg – отстояние центра тяжести судна от мидель-шпангоута, м; xf – абсцисса центра тяжести площади ватерлинии, м; xm – абсцисса теоретического шпангоута с номером m, м; Iψ – момент инерции площади ватерлинии относительно оси 
, м4; Jyy' – момент инерции массы судна относительно оси 
, т·м2; g – ускорение силы тяжести, м/с2; ρ – плотность воды, т/м3; SWL – площадь ватерлинии судна, м2; υ – скорость судна, м/с.
Следует отметить, что исходная система (1) рассматривает задачу в линейной постановке. Но при зарывании носа судна в волну качка становится нелинейной по восстанавливающему моменту [6]. Подобный эффект наблюдается и при рассмотрении вертикальной качки, где погружение палубы в воду в носовой оконечности приводит к нарушению линейной зависимости между вертикальным перемещением центра тяжести ζg и восстанавливающей силой C33ζg. Данное обстоятельство приводит к необходимости произвести корректировку отдельных элементов модели (1).
Уточнение коэффициентов модели
Вместо постоянных коэффициентов восстанавливающих сил C33 и C55 в системе уравнений (1) при учете зарывания носовой оконечности судна в волну следует использовать переменные коэффициенты 
и 
, которые с учетом изложенных выше соображений могут быть определены из выражений:
(2)
(3)
где 
– площадь ватерлинии судна в текущий момент времени, определяемая с использованием теоретического чертежа с учетом зарывания носовой оконечности в волну, м2; 
– текущее значение продольного восстанавливающего момента, определяемое на основании теоретического чертежа с учетом погружения носовой оконечности судна в воду, кН·м.
Также при входе носовой оконечности в воду следует выполнять корректировку главной части возмущающих сил и моментов, что может быть осуществлено путем использования зависящих от времени коэффициентов 
вместо постоянных F1, F2, M1, M2.
Кроме того, при входе носовой оконечности в воду может наблюдаться изменение инерционных коэффициентов. Для уточнения значений инерционных коэффициентов А33 и А55 был проведен вычислительный эксперимент с использованием метода SPH. В рамках вычислительного эксперимента определялись инерционные силы, действующие со стороны жидкости на колеблющийся контур, пересекающий поверхность жидкости, и на такой же контур, полностью погруженный в воду. Определение присоединенных масс осуществлялось аналогично тому, как это описано в работе [21] применительно к физическому эксперименту. Результаты анализа показали, что увеличение присоединенных масс на единицу длины корпуса в результате погружения носовой оконечности в воду может быть весьма существенным и достигать 250 %, таким образом вместо постоянных коэффициентов А33 и А55 можно использовать являющиеся функцией времени коэффициенты 
Однако необходимо учитывать, что это изменение происходит только на длине погруженной в воду носовой оконечности и на протяжении относительно небольшой доли периода качки. Поэтому итоговое влияние изменения присоединенных масс при зарывании носовой оконечности в волну на исследуемые параметры оказывается не столь существенным, как это будет показано ниже при рассмотрении конкретного примера.
Дополнительно в системе уравнений (1) должны быть учтены компоненты сил и моментов, связанные непосредственно с воздействием гидродинамической силы PN, вызванной обтеканием палубы судна в носовой оконечности при ее зарывании в волну, что можно сделать согласно [3, 4, 22] (рис. 1).
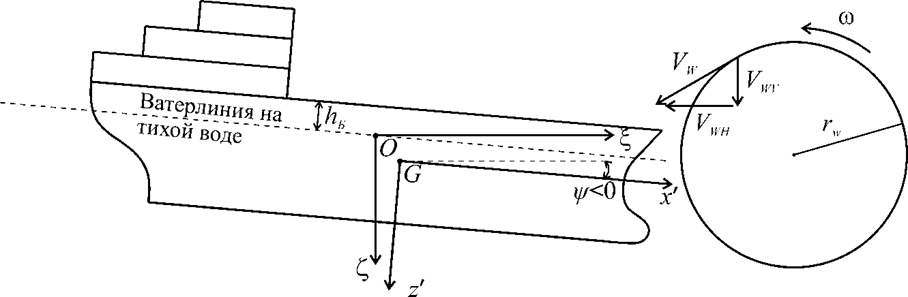
Рис. 1. Схема движения частиц воды в волне
Fig. 1. Diagram of the movement of water particles in a wave
Процедура определения результирующей скорости обтекания VR носовой оконечности представлена в [3, 4], при этом итоговое выражение имеет вид:
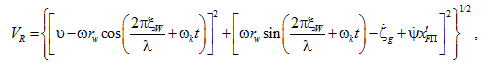
где ξW – координата, отсчитывая от миделя, начиная с которой палуба погружена в воду, м; 
– отстояние центра тяжести судна от центра тяжести погруженной части палубы, м; ωk – кажущаяся частота волны, с–1; ω – частота волны, с–1; rw – радиус орбиты на свободной поверхности воды, м.
Гидродинамическую силу и момент, действующие на носовую оконечность в условиях зарывания в волну, согласно [3, 4], можно в первом приближении определить из зависимостей
(4)
(5)
где FП – погруженная в воду площадь палубы, м2; CN – гидродинамический коэффициент.
Процедура определения указанных величин основана на использовании теоретического чертежа и рассмотрена в [3, 4].
Так как носовая оконечность представляет собой тело сложной формы, то для определения коэффициента CN, входящего в выражение (4), можно воспользоваться результатами экспериментальных исследований, приведенных в [23]. Для оценки указанного коэффициента носовая оконечность погружалась в воду на определенную глубину и буксировалась с заданной скоростью в опытовом бассейне. Подробное описание экспериментальных исследований приведено в [23]. Результаты замеров гидродинамических усилий и аппроксимация с использованием формулы (4) представлены на рис. 2.
Рис. 2. Усилия, действующие на носовую оконечность судна при ее обтекании потоком жидкости
Fig. 2. Forces acting on the bow of the vessel when it is surrounded by a liquid flow
Согласно рис. 2 формула (4) позволяет оценить гидродинамические воздействия на носовую оконечность судна при ее зарывании в волну и может быть использована для определения величины PN.
Учитывая выражение (5) и используя введенные переменные коэффициенты, можно модифицировать систему уравнений (1) для оценки величины гидродинамических нагрузок, действующих на палубу судна при ее зарывании в волну:
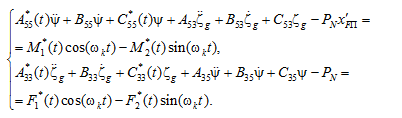(6)
Дифференциальные уравнения, входящие в систему (6), являются нелинейными, т. к. коэффициенты 
, определяемые формулами (2) и (3), содержат в неявном виде переменные ψ и ζg, а зависимость продольного восстанавливающего момента 
от угла дифферента при зарывании носовой оконечности в волну становится нелинейной. Кроме того, из-за наличия в этих уравнениях членов, содержащих PN, в них входят 
во второй степени, а также произведения этих величин. Решить систему (6) можно с использованием численных методов, например метода Рунге – Кутты.
Результаты расчета на регулярном волнении и их анализ
На рис. 3 и 4 приведены результаты расчета действующих на палубу в носовой оконечности гидродинамических сил (отнесенных к весовому водоизмещению судна D) для танкера длиной 168 м, имеющего водоизмещение 26 450 т и идущего вразрез волне. Гидродинамические нагрузки могут достигать существенных значений (при рассмотренных параметрах судна и волнения порядка 10 % от весового водоизмещения судна D, т. е. 0,1 D), что может привести к гибели судна [4, 5].
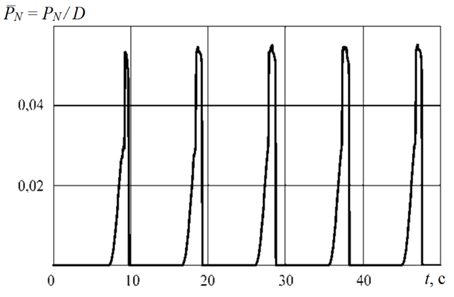
Рис. 3. Зависимость гидродинамической силы
от времени при высоте волны hw = 12 м
Fig. 3. Dependence of the hydrodynamic force
on time at wave height hw = 12 m
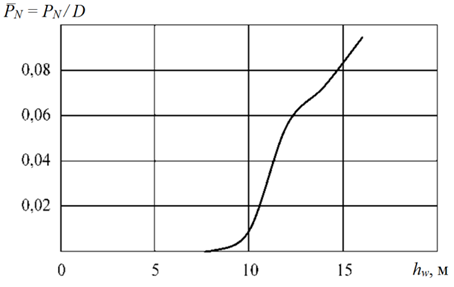
Рис. 4. Зависимость относительной величины
гидродинамической силы от высоты волны
Fig. 4. Dependence of the relative magnitude
of the hydrodynamic force on the wave height
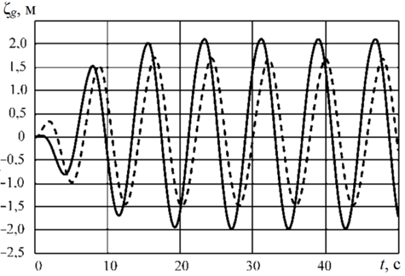
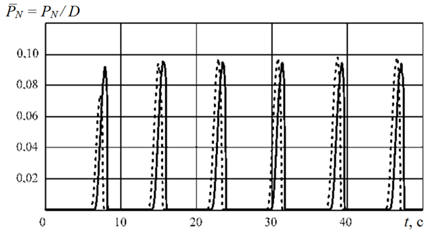
Также было проведено сопоставление результатов расчета, полученных с использованием предложенной в настоящей статье методики и в рамках упрощенного подхода [3, 16], при котором не рассматривается влияние вертикальной качки на килевую (рис. 5).
При применении указанных методик наблюдается некоторое расхождение в углах крена и дифферента, однако его влияние на величину гидродинамического давления, действующего на палубу при зарывании носовой оконечности в волну, оказывается в большинстве случаев незначительным. В связи с изложенным можно сделать вывод о том, что для моделирования динамики морских транспортных судов с традиционной формой обводов могут использоваться обе методики, причем применение упрощенной позволяет сократить затраты вычислительных мощностей.
а
б
в
Рис. 5. Сопоставление результатов расчета с использованием предложенной (сплошные линии) и упрощенной (пунктирные линии) методики:
а – килевая качка; б – вертикальная качка; в – гидродинамическая сила, действующая на носовую оконечность
Fig. 5. Comparison of the calculation results using the proposed (solid lines) and simplified (dotted lines) methodology: a – pitching; б – heaving;
в – hydrodynamic force acting on the bow of the vessel
Анализ влияния изменения величины присоединенных масс при погружении носовой оконечности в воду на исследуемые параметры позволяет утверждать, что указанное увеличение присоединенной массы в ряде случаев можно не учитывать. В рассмотренном здесь случае максимальное увеличение присоединенных масс и моментов инерции при вертикальной и килевой качке судна составило 27 и 49 % соответственно, однако это увеличение имеет место лишь на протяжении сравнительно небольшой доли периода качки. При этом в случае учета изменения присоединенных масс наблюдается падение величины гидродинамической нагрузки, действующей на палубу при ее погружении в волну, примерно на 2 %.
Учет нерегулярности волнения
Представленные выше результаты получены при моделировании динамики судна на регулярном волнении. Так как дифференциальные уравнения, входящие в систему (6), являются нелинейными, то для оценки величин нагрузок, реализуемых в условиях эксплуатации судна на нерегулярном волнении, целесообразно воспользоваться вероятностным методом расчета нелинейной качки судна и силовых воздействий на корпусные конструкции [24].
Согласно [24], на каждом из уровней амплитуд входного процесса связь между случайными амплитудами входного R и выходного Ai процессов представляется в виде:
где ki – коэффициент статистической линеаризации; Ai – амплитуда выходного процесса; – математическое ожидание выходного процесса при воздействии входного процесса с фиксированной амплитудой.
Затем зависимость между амплитудами входного и выходного процессов аппроксимируется полиномом вида:
где bj – неизвестные коэффициенты; m – порядок модели.
Согласно [24], неизвестные коэффициенты bj определяются с использованием вероятностного подхода из условия минимума дисперсии разности. После определения указанных коэффициентов плотность распределения амплитуды выходного процесса представляется в виде:
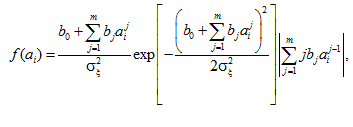
где 
– дисперсия входного процесса.
В качестве примера рассмотрим оценку изгибающих моментов на миделе судна с учетом зарывания носовой оконечности в волну в условиях 7-балльного волнения. При этом изгибающий момент Ммид целесообразно привести к безразмерному виду, отнеся его к предельному моменту для миделевого сечения корпуса:
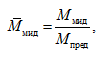
где Мпред – предельный момент для миделевого сечения, кН·м.
Плотность распределения амплитуд изгибающих моментов на миделе судна 
представлена на рис. 6. Кривая 2 представляет собой плотность распределения волнового изгибающего момента Мw в соответствии с [25] (без учета эффекта зарывания в волну и в линейной постановке), т. е. при ее построении принималось Ммид = Мw. Кривая 1 соответствует сумме волнового изгибающего момента Мw (определенного указанным выше способом) и дополнительного изгибающего момента Мдоп, вызванного воздействием гидродинамической силы на палубу в носовой оконечности судна при ее зарывании в волну (Ммид = Мw + Мдоп).
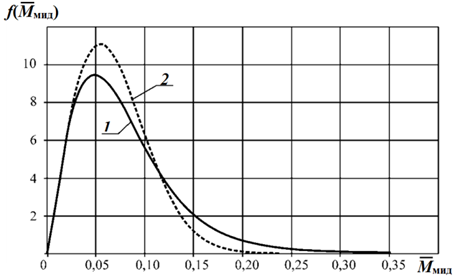
Рис. 6. Плотности распределения амплитуд изгибающих моментов в миделевом сечении судна
Fig. 6. Distribution densities of bending moment amplitudes in the ship's midsection
Видно, что при зарывании носовой оконечности в волну (кривая 1) центр тяжести кривой смещается вправо, при этом несколько снижается вероятность возникновения изгибающих моментов в диапазоне 
и одновременно существенно повышается их вероятность при 
, что свидетельствует о необходимости учета явлений, возникающих при зарывании носовой оконечности судна в волну, при оценке прочности судна.
Выводы
1. В статье представлена уточненная математическая модель, основанная на полной системе дифференциальных уравнений [20], c помощью которой можно рассчитывать значения гидродинамических сил, действующих на палубу при зарывании носовой оконечности судна во встречную волну.
2. Для решения рассматриваемых задач можно использовать как упрощенную [3, 16], так и более точную модель, представленную в настоящей статье.
3. Изменением присоединенных масс при зарывании носовой оконечности в волну в ряде случаев можно пренебречь.
4. Разработанная модель может применяться для оценки величины изгибающих моментов в корпусе судна в случае нерегулярного волнения.
1. Barabanov N. V., Ivanov N. A., Novikov V. V., Shemendiuk G. P. Povrezhdeniia i puti sovershenstvovaniia su-dovykh konstruktsii [Damage and ways to improve ship structures]. Leningrad, Sudostroenie Publ., 1989. 256 p.
2. Ivanov H. A., Kalenchuk S. V. Modelirovanie gidrodinamicheskikh nagruzok, vyzyvaiushchikh povrezhdeniia nosovykh palubnykh konstruktsii. Korablestroenie i okeanotekhnika. Problemy i perspektivy [Simulation of hydro-dynamic loads causing damage to bow deck structures. Shipbuilding and ocean engineering. Problems and prospects]. Materialy Mezhdunarodnoi konferentsii (Vladivostok, 14–17 sentiabria 1998 g.). Vladivostok, Izd-vo DVG-TU, 1998. Vol. 1. Pp. 291-294.
3. Burakovskii E. P., Burakovskii P. E. K voprosu ob opredelenii nagruzki, deistvuiushchei na palubu sudna v nosovoi okonechnosti pri ee zalivanii na vstrechnom volnenii [On the issue of determining the load acting on the deck of a vessel in the bow tip when it is flooded in an oncoming wave]. Morskie intellektual'nye tekhnologii, 2018, no. 4-3 (42), pp. 19-25.
4. Burakovskii E. P., Burakovskii P. E., Dmitrovskii V. A. Konstruktivnoe obespechenie bezopasnosti moreplavaniia: monografiia [Constructive provision of navigation safety: monograph]. Saint Petersburg, Lan' Publ., 2020. 300 p.
5. Burakovskii P. E. Issledovanie ostoichivosti sudna v usloviiakh zakhvata volnoi nosovoi okonechnosti [Investigation of the stability of a vessel under conditions of wave capture of the bow tip]. Vestnik Astrakhanskogo gosudarstvennogo tekhnich-eskogo universiteta. Seriia: Morskaia tekhnika i tekhnologiia, 2018, no. 2, pp. 7-13.
6. Blagoveshchenskii S. N. Kachka korablia [Rolling of the ship]. Leningrad, Sudpromgiz, 1954. 520 p.
7. Kawakami M. On the Impact Strength of Ships Due to Shipping Green Seas. Journal of the Society of Naval Architects of Japan, 1969, vol. 125, pp. 99-106.
8. Liu Zh., Wan D. Numerical simulation of green water on S-175 containership. Proceedings of the Second Conference of Global Chinese Scholars on Hydrodynamics, Nov. 11-14, 2016. Wuxi, China, China Ocean Press, 2016. Pp. 815-821.
9. Gomez-Gesteira M., Cerqueiro D., Crespo C., Dalrymple R. A. Green water overtopping analyzed with a SPH model. Ocean Engineering, 2005, no. 32, pp. 223-238.
10. Kleefsman K. M. T., Loots G. E., Veldman A. E. P., Buchner B., Bunnik T., Falkenberg E. The numerical simulation of green water loading including vessel motions and the incoming wave field. Proceedings of OMAE 2005 24th International Conference on Offshore Mechanics and Arctic Engineering (OMAE 2005), June 12-17, 2005. Halkidiki, Greece, American Society of Mechanical Engineers, 2005. Pp. 981-992.
11. Touzé D., Marsh A., Oger G., Guilcher P.-M., Khaddaj-Mallat C., Alessandrini B., Ferrant P. SPH simulation of green water and ship flooding scenarios. Journal of Hydrodynamics, 2010, no. 22 (5), pp. 231-236.
12. Ersdal G., Kvitrud A. Green Water on Norwegian Production Ships. Proceedings of the Tenth International Offshore and Polar Engineering Conference Seattle, May 28 – June 2, 2000. USA, ISOPE Publ., 2000. Pp. 211-218.
13. Bulk carrier safety. Sensitivity of wetness and deck loads to bow height and forward buoyancy reserves in extreme weather conditions (MSC 71/4/4). IMO Maritime Safety Committee. London, IMO Publ., 1999. 43 p.
14. Buchner B., Cozjin J. L. An investigation into the numerical simulation of green water. 8th International Conference on the Behaviour of Offshore Structures (BOSS’97). The Netherlands, Delft, Pergamon Press, 1997, vol. 2, pp. 113-125.
15. Standing R. G. Green Seas damage an FPSOs and FSUs. HSE report OTH 486. London, Health & Safety Executive Publ., 1997. 36 p.
16. Blagoveshchenskii S. N., Kholodilin A. N. Spravochnik po statike i dinamike korablia: v 2-kh tomakh. Vol. 2. Di-namika (kachka) korablia [Handbook of Ship Statics and Dynamics: in 2 volumes. Vol. 2. The dynamics (pitching) of the ship]. Leningrad, Sudostroenie Publ., 1976. 176 p.
17. Monaghan J. J. Smoothed particle hydrodynamics. Annual Reviews of Astronomy and Astrophysics, 1992, no. 30, pp. 543-574.
18. Burakovskii P. E. Issledovanie vliianiia konstruktivnykh elementov na gidrodinamicheskie sily i momenty, deistvuiush-chie na nosovuiu okonechnost' sudna v usloviiakh ee zaryvaemosti, s ispol'zovaniem tekhnologii Smoothed Particle Hydrodynamics (SPH) [Investigation of the influence of structural ele-ments on the hydrodynamic forces and moments acting on the bow tip of the vessel under conditions of its burrowing, using Smoothed Particle Hydrodynamics (SPH) technology]. Morskie intellektual'nye tekhnologii, 2022, no. 4-3 (58), pp. 39-45.
19. Sistemy iskusstvennogo intellekta v intellektual'nykh tekhnologiiakh I veka [Artificial intelligence systems in intelligent technologies of the 21st century]. Pod redaktsiei Iu. I. Nechaeva. Saint Petersburg, Art-Ekspress Publ., 2011. 375 p.
20. Morekhodnost' sudov i sredstv okeanotekhniki. Metody otsenki: monografiia [Seaworthiness of ships and ocean equip-ment. Assessment methods: monograph]. Pod redaktsiei I. K. Borodaia. Saint Petersburg, Izd-vo Krylovskogo gosudarstvennogo nauchnogo tsentra, 2013. 256 p.
21. Kim D. J., Lee G. J., Kwon Ch. S., Kim Y. G., Park J.-Y., Jun B.-H. Added Mass of Submerged Bodies Obtained by Forced Oscillation Tests and Numerical Calculations of Potential Flow. Journal of the Society of Naval Architects of Korea, 2022, vol. 59, no. 4, pp. 214-224.
22. Shuleikin V. V. Fizika moria [Physics of the sea]. Moscow, Nauka Publ., 1968. 1080 p.
23. Burakovskii P. E. Eksperimental'noe issledovanie gidrodinamicheskikh sil, deistvuiushchikh na nosovuiu oko-nechnost' sudna v protsesse zakhvata ee volnoi [Experimental study of hydrodynamic forces acting on the bow tip of a vessel during its capture by a wave]. Trudy Krylovskogo gosudarstvennogo nauchnogo tsentra, 2019, iss. 1, pp. 146-152.
24. Kryzhevich G. B. Veroiatnostnyi metod rascheta nelineinoi kachki sudna i silovykh vozdeistvii na korpusnye konstruktsii [A probabilistic method for calculating nonlinear ship pitching and force effects on hull structures]. Su-dostroenie, 1999, no. 6, pp. 11-15.
25. Volkov V. M. Prochnost' korablia [Ship strength]. Nizhnii Novgorod, Izd-vo NGTU, 1994. 260 p.
