from 01.01.2010 until now
Russian Federation
Russian Federation
Russian Federation
In the tasks of analyzing economic or biometric data, the Hurst indicator is a functional that does not work well on small samples, which is primarily caused by the fact that it does not feel which positively or negatively corre-lated data it analyzes. It is assumed that it is possible to make the Hurst indicator sensitive to the trend sign of the analyzed data if it is evaluated separately for positive and negative regression. The aim of the article is to eliminate the uncertainty of the empirical Hurst index through reflections of values to the right and/or left of the centre of its scale. The neural network approach to estimating the regression sign of unrelated data is considered, which is based on the use of three different statistical criteria. The first criterion is based on the estimation of the mutual location of the minimum and maximum values in the analyzed sample. The second criterion is the sign of the correlation coefficient calculated by the classical Pearson-Edgeworth-Edleton formula of the late 19th century. The third criterion is the accumulated sum of differences of adjacent samples of a small sample. It is shown that the selected criteria can be represented as a network of three binary neurons responding with an output code with threefold code redundancy. Elimination of threefold redundancy of the output code allows to raise the level of reliability of the decisions made on small samples consisting of 21 experiments. The software implementation of the numerical experiment and statistical distributions of output state values of three used criteria are given. It is shown that the correlation of the responses of the three criteria considered in the paper is significantly less than the unit correlation: 0.31; 0.51; 0.61. This allows to raise the accuracy of predicting the value of the sign of the Hurst neuron index for a small sample.
small samples, empirical Hurst index, regression sign, neural network, neuron, statistical criterion
Общие положения нейросетевого статистического анализа
В XX в. исследователи математической статистики создали 21 статистический критерий для проверки гипотезы независимости [1]. К сожалению, все созданные ранее статистические критерии хорошо работают на больших выборках и плохо работают на малых. Так, классический критерий χ2 Пирсона [2] дает приемлемые для практического применения результаты на выборках в 160 и более опытов. При решении практических задач биометрии и экономики приходится использовать выборки существенно меньшего объема – примерно в 10 раз.
Проблема может быть преодолена параллельным применением нескольких статистических критериев при анализе одной и той же малой выборки. При этом таблицы доверительных вероятностей для каждого из статистических критериев будут разными, для их совмещения необходимо решать сложную техническую задачу приведения разных шкал доверительной вероятности к одной шкале.
Более простым путем решения задачи является совмещение шкал доверительной вероятности разных критериев в одной точке. Для этого требуется каждый из объединяемых статистических критериев представить бинарным нейроном. Тогда объединение их в одну нейросеть будет давать выходной бинарный код с некоторой избыточностью [3, 4]. Устранить кодовую избыточность можно с использованием любого самокорректирующегося кода [5]. Как правило, в момент устранения кодовой избыточности обнаруживаются и устраняются противоречащие друг другу кодовые состояния (ошибочные кодовые состояния). В итоге доверительная вероятность к принимаемым нейросетью решениям увеличивается.
Формально мы можем использовать нейросеть, объединяющую 21 статистический критерий XX в. [1], в этом случае мы получим выходные бинарные коды с 21-кратной избыточностью, т. е. появляется возможность многократного увеличения доверительной вероятности нейросетевой проверки гипотезы независимости малых выборок. В справочнике [4] приведены новые 178 критериев, которые синтезированы уже в начале XXI в., т. е. теоретически мы можем получать сети из 199 искусственных нейронов, способные давать достаточно достоверные оценки проверки гипотезы независимости малых выборок.
Еще одним важным теоретическим моментом является перспектива увеличения числа проверяемых нейросетью гипотез [6]. Если мы используем сети из 199 бинарных нейронов, то проверяем только одну гипотезу r(x, y) ≈ 0,00. Если мы переходим к использованию искусственных нейронов с выходными троичными квантователями, то у нас появляется возможность обучить нейросеть так, чтобы параллельно проверять уже 3 гипотезы: r(x, y) ≈ ≈ {–0,10; 0,00; +0,10}. Нашим соотечественником А. Ю. Хренниковым было доказано, что при нейросетевом анализе выгодно использовать нейроны с p-арными квантователями, т. е. число устойчивых выходных состояний квантователей должно совпадать с простыми числами p = {2, 3, 5, 7, 11, ...} [7, 8]. Формальная замена 199 бинарных нейронов на 199 троичных будет эквивалентна тому, что верно обученная нейросеть будет выполнять балансировку 199 шкал доверительной вероятности уже в двух точках. При использовании 11-ричных нейронов верно обученная нейросеть будет давать возможность надежно проверять 10 гипотез, согласуя при этом 199 шкал доверительных вероятностей всех 199 искусственных нейронов.
Фактически мы уже имеем промышленную технологию применения больших сверточных двухслойных нейронных сетей. Каждый из 199 нейронов первого слоя будет вычислять свертку по заранее заданному статистическому критерию для проверки одной из 10 статистических гипотез, а второй слой должен выполнять функцию свертывания избыточности выходных 11-арных кодов.
Проблема доверия к множеству статистических критериев, применяемых при обобщенном нейросетевом анализе малых выборок биометрических данных и данных рынка
Одной из проблем применения нейросетевой обработки реальных данных является низкий уровень доверия к новому инструменту. В частности, уровень доверия специалистов по биометрии к 21 классическому статистическому критерию XX в. [1] выше, чем к новым 178 статистическим критериям начала XXI в. [3]. Положение усугубляется тем, что для части задач биометрии и экономики нет заранее созданных тестовых примеров.
В этом контексте значительный интерес представляют давно синтезированные и активно используемые на практике статистические критерии. Для экономики к ним можно отнести эмпирический критерий Хёрста [9–11]. К сожалению, он, как и другие статистические критерии, плохо работает на малых выборках. Так, при выборках в 21 опыт оценка эмпирического показателя Хёрста Xr содержит значительную методическую ошибку, которая может быть устранена [12]:
 (1)
(1)
где Rs(x) – размах данных в малой выборке объемом в 21 опыт; σ(x) – стандартное отклонение малой выборки; 0,077 – аддитивный компенсатор методической погрешности для малой выборки в 21 опыт.
Еще одной проблемой является то, что эмпирический показатель Хёрста (1) не способен различать персистентные данные, когда он находится в интервале от 0,5 до 1,0, и антиперсистентные данные, когда он должен находиться в интервале от 0,0 до 0,5. Последнее связано с тем, что размах данных Rs(x) = max(x) – min(x) и стандартное отклонение σ(x) всегда являются положительными величинами, а нормированный логарифм их отношения (1) почти всегда больше 0,5, но меньше 1,0.
Получается, что показатель Хёрста относится к корреляционным функционалам, которые не чувствуют того, какие данные они анализируют (положительно коррелированные или отрицательно коррелированные). Если объем анализируемой выборки значителен (выборка накрывает сотни трендов поведения рынка «быки»/«медведи»), то отсутствием подобной чувствительности можно пренебречь.
В этом случае человек, выполняющий статистический анализ по косвенным данным, должен принять решение о состоянии анализируемых данных (персистентные или антиперсистентные).
Ситуация меняется, когда анализируются малые выборки. В этом случае отсутствие чувствительности к знаку анализируемых трендов приводит формулу (1) к появлению значительной методической погрешности. Устранить эту погрешность возможно, если сделать показатель Хёрста чувствительным к знаку тренда анализируемых данных. В этом случае следует раздельно оценивать показатель Хёрста для положительной регрессии «быки» (рост цен на рынке) и отрицательной регрессии «медведи» (падение цен на рынке). Предполагается, что именно раздельное оценивание значений эмпирического показателя Хёрста позволит снизить уровень нестационарности данных рынка [11]. В свою очередь, доверие к эмпирическому показателю (1) обусловлено тем, что для него из ряда теоретических положений вытекает простое соотношение между нормированной энтропией E(r) данных рынка, корреляционной сцепленностью r между ними и показателем Хёрста Xr (рис. 1).
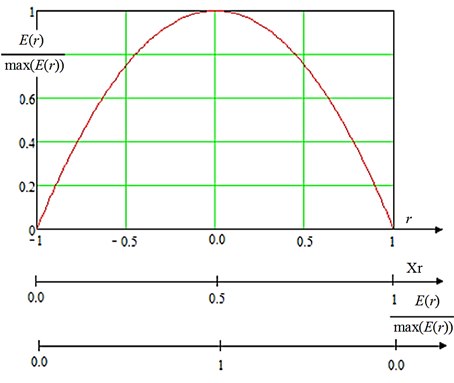
Рис. 1. Теоретически ожидаемая связь метрики эмпирического показателя Хёрста Xr,
коэффициента корреляционной сцепленности r анализируемых данных и нормированного значения
энтропии E(r) данных малой выборки
Fig. 1. Theoretically expected relationship between the empirical Hurst metric Xr, the correlation coefficient r
of the analyzed data and the normalized entropy value E(r) of the small sample data
Принципиально важным является то, что распределение показателя Хёрста должно быть близко к распределению энтропии, т. е. формально в уравнениях, где возникает энтропия, ее можно заменить в первом приближении показателем Хёрста. Именно это обстоятельство и обуславливает внимание к работам, связанным с показателем Хёрста.
Программное моделирование значений связи показателя Хёрста с показателем корреляционной сцепленности анализируемых данных
Эффект появления методической ошибки при оценке показателя Хёрста на малой выборке в 21 опыт иллюстрирует рис. 2.
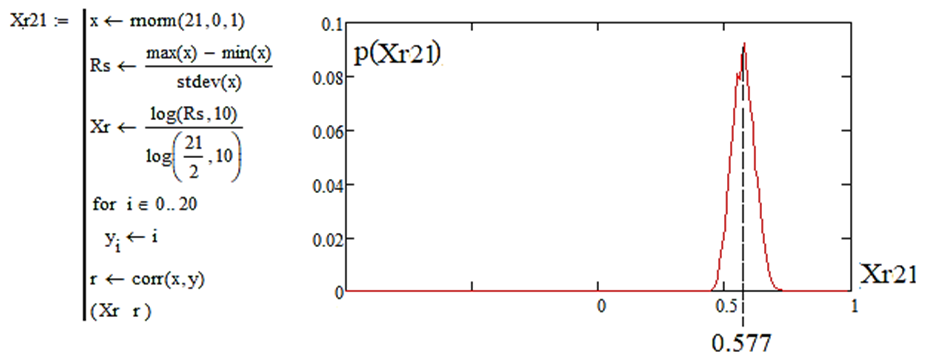
Рис. 2. Появление методической ошибки со значением +0,077
при моделировании показателя Хёрста для независимых исходных данных выборок объемом в 21 опыт
Fig. 2. Occurrence of a methodological error with the value of +0.077
during Hurst's index modelling for independent initial data of 21 samples
В левой части рис. 2 приведена программа, моделирующая данные показателя Хёрста на языке программирования MathCAD для малых выборок в 21 опыт с нормальным распределением, нулевым математическим ожиданием и единичным стандартным отклонением. В правой части рис. 2 приведено распределение значений показателя Хёрста. Из этого распределения следует, что его математическое ожидание составляет значение 0,577. Это существенно больше того, что предсказывает теория. Появляется существенная методическая ошибка порядка 15,4 %. Ее необходимо компенсировать, как это показано в формуле (1), тогда положение меняется и математическое ожидание распределения данных точно совпадает с теоретическим, как это отображено на рис. 1. Численным моделированием можно показать, что вычисление показателя Хёрста по формуле (1) будет приводить к смещению математического ожидания в сторону его увеличения при любом росте модуля корреляционной сцепленности [12]. Само значение показателя корреляционной сцепленности данных в нашем случае совпадает с вычислением коэффициента корреляции по классической формуле Пирсона – Эджуорта – Эдлтона конца XIX в.:
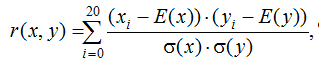
где xi – анализируемая последовательность данных; yi – номера последовательности поступления анализируемых данных; E(.) – функционал вычисления математического ожидания; σ(.) – функционал вычисления стандартного отклонения. Так как нам необходимо сделать показатель Хёрста (рис. 3, а) чувствительным к знаку коэффициента корреляции, мы можем создать формальный нейрон, анализирующий знаки коэффициента корреляции sign(r(x, y)). На рис. 3, б приведены состояния формального нейрона sign(r(x, y)).
К сожалению, формальный нейрон-предсказа-тель знака регрессии sign(r(x, y)) не может быть применен в одиночку. Вероятность ошибок его предсказаний слишком велика и составляет 0,5.
В связи с этим необходимо использовать несколько подобных нейронов, построенных на других критериях оценки знака регрессии.
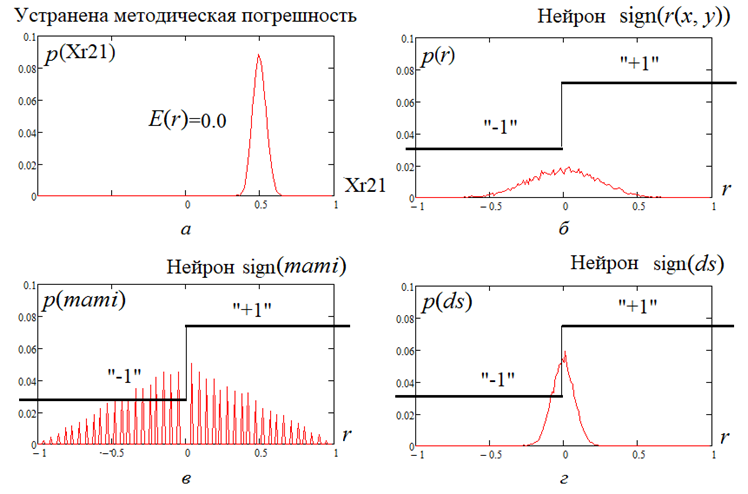
Рис. 3. Отклики трех формальных нейронов, используемых для оценки знака регрессии анализируемых данных
показателем Хёрста: а – распределение показателя Хёрста с устраненной методической погрешностью;
б – отклики формального нейрона sign(r(x, y)); в – отклики формального нейрона mami; г – отклики формального нейрона dS
Fig. 3. Responses of three formal neurons used to estimate the sign of the regression of the analyzed data using
the Hurst index: а – distribution of the Hurst index with eliminated methodological error; б – responses of the formal
neuron sign(r(x, y)); в – responses of the formal neuron mami; г – responses of the formal neuron dS
В качестве второго статистического критерия предсказания знака регрессии воспользуемся оценкой расстояния между max(x) и min(x) в анализируемой последовательности:
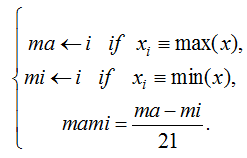 (2)
(2)
Критерий знака регрессии (2) является дискретным, распределение амплитуд вероятностей его значений приведено на рис. 3, в. Очевидно, что этот, как и предыдущий, критерий коэффициентов корреляции, может быть преобразован в формальный бинарный нейрон sign(mami), откликающийся состоянием «–1» и «+1». К сожалению, как и предыдущий формальный нейрон, этот новый нейрон работает с высокой вероятностью ошибок первого и второго рода P1 = P2 = 0,5. Тем не менее два этих нейрона уже могут использоваться в паре, т. к. отклики их базовых критериев слабо коррелированны: corr(r, mami) ≈ 0,31.
Отметим, что простейшие коды, свертывающие кодовую избыточность откликов нейросети [3, 4, 6], должны иметь нечетное число разрядов, т. е. необходим еще один статистический критерий оценки знака регрессии. В качестве такого критерия воспользуемся накоплением разностей соседних отсчетов:
 (3)
(3)
Опираясь на статистику (3), легко построить формальный нейрон предсказания знака регрессии sign(ds). Его вероятностные характеристики отображены на рис. 3, г.
Как и предыдущие нейроны, его нельзя использовать отдельно из-за высоких значений вероятностей ошибок первого и второго рода P1 = P2 = 0,5. Однако он пригоден для использования совместно с двумя предыдущими нейронами, т. к. их отклики имеют существенную независимую составляющую: corr(r, dS) ≈ 0,51 и corr(mami, dS) ≈ 0,61. Избыточность откликов трех описанных выше предсказывающих нейронов должна быть свернута суммированием их состояний:
![]() (4)
(4)
Четвертый свертывающий нейрон формально строится, как и три предыдущих, анализом знака суммы (4): sign(mmm). Столь простая операция позволяет существенно снизить вероятности ошибок первого и второго рода двухслойной нейросети P1 = P2 = 0,347. Для того чтобы оценить требуемое число нейронов предсказания знака регрессии данных показателя Хёрста, воспользуемся линейной экстраполяцией в логарифмических координатах. Результаты экстраполяции отображены на рис. 4.
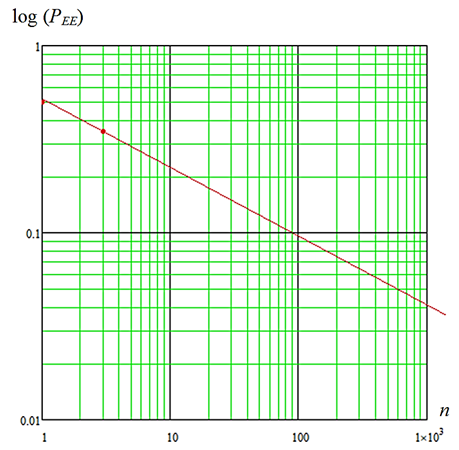
Рис. 4. Предсказание снижения вероятности ошибок первого и второго рода P1 = P2 = PEE
ростом числа искусственных нейронов, оценивающих знак регрессии
Fig. 4. Prediction of a decrease in the probability of errors of the first and second kind P1 = P2 = PEE
by increasing the number of artificial neurons estimating the regression sign
Таким образом, при использовании 11 нейронов мы должны ожидать снижения вероятностей ошибок до значения P1 = P2 = PEE ≈ 0,21. Если удастся воспользоваться сетью из 101 нейрона, то вероятности ошибок должны снизиться до величины P1 = P2 = PEE ≈ 0,1. При использовании 1 001 нейронов ожидается снижение вероятностей до значения P1 = P2 = PEE ≈ 0,05. Подобные прогнозы построены на использовании трех самых простых статистических критериев. Предположительно, поиск более эффективных нейронов должен приводить к существенному росту доверия к принимаемым нейросетевым решениям. То же самое относится и к более эффективным процедурам свертывания нейросетевой кодовой избыточности [13].
Тем не менее, даже опираясь на предсказатель знака регрессии, состоящий только из трех нейронов sign(mmm), мы уже можем частично сделать эмпирический показатель Хёрста чувствительным к знаку регрессии его данных:
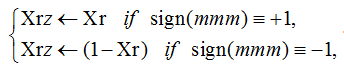 (5)
(5)
где Xrz – эмпирический показатель Хёрста, частично чувствительный к знаку регрессии.
Если предположить, что нестационарность оценок показателя Хёрста на малых выборках [11] целиком определяется нестабильностью знака регрессии данных, то преобразования вида (5) должны ощутимо снизить наблюдаемые эффекты нестационарности.
Оценка нестационарности вариаций размаха цен на палладий
Рассмотрим в качестве примера данные котировок цен на палладий за период 01.01.2021–01.03.2025 (исходные данные взяты с финансового портала ЦБ РФ [14]). Объем всех данных составляет 1 027 значений. Для всей выборки показатель Хёрста с устраненной методической ошибкой [12] равен 0,563.
Классика
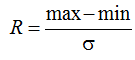
имеет существенную нестационарность, которую можно оценить через вычисление размаха по окну в 21 опыт со сдвигом на один отсчет. Итого для 1 027 отсчетов цен палладия получим (1 027 – 21) + + 1 = 1 007 отсчетов R. По ним вычисляем σ(R) – это базовая оценка нестационарности классического показателя Хёрста по палладию.
Разбиваем данные классического показателя на две группы:
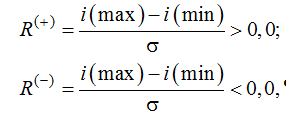
где i(min) – индекс (номер) минимального значения; i(max) – индекс (номер) максимального значения.
Если знак показателя вносит свою собственную существенную нестационарность, то разделение классической нестационарности на 2 компонента должно приводить к следующим соотношениям: σ(R(+)) ≈ σ(R(–)) < σ(R). Полученные расчетные значения σ(R(+)) = 0,0488, σ(R(–)) = 0,0405, σ(R) = 0,4813 для нашей выборки подтверждают этот факт.
Предложенный в статье подход позволяет ослабить влияние нестационарности оценок эмпирического показателя Хёрста на малых выборках.
В нашем случае показатель роста стационарности определяется соотношениями

и
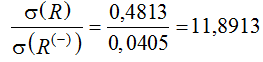 .
.
То, что исходная последовательность нормированных размахов (статистической основы показателя Хёрста) имеет показатель нестационарности примерно в 10 раз выше, чем частные показатели, свидетельствует о переключении рынка с участков «медведи» на участки «быки», является одной из основных причин нестационарности показателя Хёрста. Появляется реальная возможность подавлять нестационарность показателя Хёрста не только за счет значительного увеличения объема выборки обрабатываемых данных, но и за счет синхронизации малых выборок с показателем знака регрессии данных.
Заключение
Классический показатель Хёрста не чувствителен к знаку корреляционной связи, и если пользоваться только им, то персистентные и антиперсистентные временные ряды неразличимы. В работе на примере малых выборок рассмотрена возможность снижения вероятности ошибок эмпирического показателя Хёрста за счет анализа корреляционной сцепленности данных выборки. В частности, предлагается данный функционал Хёрста совместить со шкалами доверительной вероятности разных критериев в одной точке, а затем каждый из статистических критериев представить формальным бинарным нейроном. В качестве таких бинарных нейронов в работе были выбраны знак коэффициента корреляции, знак оценки расстояния между максимальным и минимальным значениями выборки, знак накопления разностей соседних отсчетов. Безусловно, эффекты нестационарности реально наблюдаемых данных могут быть снижены за счет расширения перечня и количества используемых статистических критериев, применяемых при обобщенном нейросетевом анализе.
1. Kobzar' A. I. Prikladnaya matematicheskaya statistika. Dlya inzhenerov i nauchnyh rabotnikov [Applied mathematical statistics. For engineers and researchers]. Moscow, FIZMATLIT Publ., 2006. 816 p.
2. R 50.1.037–2002. Rekomendacii po standartizacii. Prikladnaya statistika. Pravila proverki soglasiya opytnogo raspredeleniya s teoreticheskim. Chpast' I. Kriterii tipa χ2 [P 50.1.037–2002 Recommendations on standardization. Applied statistics. Rules for verifying the agreement of an experimental distribution with a theoretical one. Part I. Criteria of type χ2]. Moscow, Gosstandart Rossii Publ., 2001. 140 p.
3. Ivanov A. I., Zolotareva T. A. Iskusstvennyj intellekt v zashchishchennom ispolnenii: sintez statistiko-nejrosetevyh avtomatov mnogokriterial'noj proverki gipotezy nezavisimosti malyh vyborok biometricheskih dannyh [Artificial intelligence in secure execution: synthesis of statistical and neural network automata for multi-criteria verification of the hypothesis of independence of small samples of biometric data]. Penza, Izd-vo PGU, 2020. 105 p.
4. Ivanov A. I. Nejrosetevoj mnogokriterial'nyj statis-ticheskij analiz malyh vyborok. Proverka gipotezy nezavisimosti: spravochnik [Neural network multic-riteria statistical analysis of small samples. Testing the Independence hypothesis: a reference book]. Penza, Izd-vo PGU, 2022. 218 p.
5. Morelos-Saragosa R. Iskusstvo pomekhoustojchivogo kodirovaniya [The art of noise-resistant coding]. Moscow, Tekhnosfera Publ., 2007. 320 p.
6. Ivanov A. I., Godunov A. I., Malygina E. A., Papusha N. A., Ermakova A. I. Nejrosetevoj analiz malyh vyborok s ispol'zovaniem bol'shogo chisla statisticheskih kriteriev dlya proverki posledovatel'nosti gipotez o znachenii matematicheskih ozhidanij koefficientov korrelyacii [Neural network analysis of small samples using a large number of statistical criteria to test the sequence of hy-potheses about the value of mathematical expectations of correlation coefficients]. Izvestiya vysshih uchebnyh zavedenij. Povolzhskij region. Tekhnicheskie nauki, 2024, no. 3, pp. 37-46. DOI:https://doi.org/10.21685/2072-3059-2024-3-4.
7. Hrennikov A. Yu. Modelirovanie processov myshleniya v p-adicheskih sistemah koordinat [Modeling of thinking processes in padic coordinate systems]. Moscow, FIZMATLITPubl., 2004. 296 p.
8. Hrennikov A. Yu. Vvedenie v kvantovuyu teoriyu informacii [Introduction to the quantum theory of infor-mation]. Moscow, FIZMATLIT Publ., 2016. 284 p.
9. Najman E. Kak pokupat' deshevo i prodavat' dorogo: posobie dlya razumnogo investora [How to buy cheap and sell expensive: a guide for a smart investor]. Moscow, Al'pina Pablisherz, 2011. 552 p.
10. Peters E. E. Chaos and Order in the Capital Mar-kets: A New View of Cycles, Prices, and Market Volatility. Wiley, 1996. 288 p. (Russ. ed.: Peters E. Haos i poryadok na rynkah kapitala. Novyj analiticheskij vzglyad na cikly, ceny i izmenchivost' rynka / per. s angl. M.: Mir, 2000. 333 s.).
11. Orlov Yu. N., Osminin K. P. Nestacionarnye vremennye ryady. Metody prognozirovaniya s primeneniem analiza finansovyh i syr'evyh rynkov [Non-stationary time series. Forecasting methods using analysis of financial and commodity markets]. Moscow, LENAND Publ., 2023. 384 p.
12. Ivanov A. I., Tarasov D. V., Ermakova A. I. Pro-grammnoe vosproizvedenie korrelyacionnyh svyazej v malyh vyborkah pri statisticheskom analize biometricheskih dannyh i dannyh rynka v prostranstve znachenij empiricheskogo pokazatelya Hyorsta [Software reproduction of correlations in small samples in the statistical analysis of biometric data and market data in the space of values of the empirical Hearst indicator]. Trudy MAI, 2024, no. 137. Available at: https://trudymai.ru/published.php?ID=181892 (accessed: 20.09.2024).
13. Volchihin V. I., Ivanov A. I., Bezyaev A. V., Filipov I. A. Raspoznavanie malyh vyborok s zadannym raspredeleniem dannyh pri ispol'zovanii iskusstvennyh nejronov, predskazyvayushchih doveritel'nye veroyatnosti sobstvennyh reshenij [Recognition of small samples with a given data distribution using artificial neurons that predict the confidence probabilities of their own decisions]. Izvestiya vysshih uchebnyh zavedenij. Povolzhskij region. Tekhnicheskie nauki, 2023, no. 4, pp. 31-39. DOI:https://doi.org/10.21685/2072-3059-2023-4-3.
14. CB RF – kursy dragmetallov [Central Bank of the Russian Federation – precious metals rates]. MFD.RU. Available at: https://mfd.ru/centrobank/preciousmetals/?left=3&right=3&from=01.01.2021&till=01.03.2025 (accessed: 20.08.2024).