Russian Federation
Russian Federation
With the development of technology, the volume of online commerce is increasing, highlighting the need for analysis and forecasting of the traffic to informational web resources. The article examines various tools for collecting and analyzing web traffic, such as Google Analytics, Yandex.Metrica, Adobe Analysis, LiveInternet, and ClickTale. Based on the analysis of the data obtainable from these sources, key metrics for forecasting traffic were identified. The metrics were grouped by qualitative and quantitative characteristics. Quantitative metrics were used for forecasting with statistical models, while qualitative metrics served as descriptive fields for the series forecasted using machine learning. For example, traffic, views, and depth of visit were identified as quantitative variables, while events, sessions, bounce rate, goals, conversions, traffic sources, and returns were classified as qualitative. Additionally, both statistical models for forecasting web traffic and models using machine learning were constructed and analyzed. The models used included SARIMA (Seasonal Autoregressive Integrated Moving Average), the Holt–Winters model, and an autoregressive model with gradient boosting. This analysis allowed for a comparison of the accuracy of the models using criteria such as mean squared error, root mean squared error, and mean absolute error. In conclusion, the gradient boosting model demonstrated the lowest average error rates, indicating the highest accuracy; however, for some series, statistical models showed greater accuracy, suggesting the need for a combination of models to achieve the most optimal results.
prediction, traffic, web resources, traffic metrics, time series, statistical methods, machine learning
Введение
Статья посвящена новым цифровым технологиям, которые используются с целью анализа и прогнозирования посещаемости информационных веб-ресурсов.
За последние 10 лет российский рынок интернет-торговли вырос в 11 раз [1]. Крупные предприятия уделяют возрастающее внимание цифровому присутствию на интернет-ресурсах, что подчеркивает важность анализа подобного рода данных. В данном исследовании проанализированы различные методы прогнозирования, на основе которых можно сделать вывод о дальнейшей посещаемости веб-ресурса, а также возможный набор данных, которые используются для решения этой задачи. Цель исследования – систематизация и оценка современных методов прогнозирования посещаемости веб-ресурсов.
В связи с увеличением рынка интернет-торговли и популяризацией данного способа ведения бизнеса крупные предприятия все чаще осознают необходимость активного присутствия в цифровом пространстве, что подчеркивает важность использования современных цифровых технологий для обработки и анализа данных. Для анализа необходимо понимать возможные источники данных и их структуру. В работе [2] выделены 5 основных ресурсов сбора данных для веб-аналитики: GoogleAnalytics, Яндекс.Метрика, AdobeAnalysis, Liveinternet, ClickTale.
Из вышеуказанных источников можно собрать данные по следующим метрикам:
– трафик: общее количество человек, которые посетили сайт за определенное время;
– просмотры: количество страниц сайта, которые пользователи открыли или обновили;
– глубина просмотра: количество просмотренных страниц за один визит. Глубина просмотра рассчитывается как отношение общего количества просмотров к количеству визитов;
– события: взаимодействие пользователей с элементами сайта. Например, заполнение формы, воспроизведение видео, скачивание прайс-листа, копирование поля e-mail;
– сеанс: визит пользователем сайта. Все взаимодействия с сайтом, просмотры страниц и различные события за время нахождения считаются как один визит;
– отказы: процент тех посещений, когда пользователи сразу ушли с сайта или посмотрели только одну его страницу, не совершив целевого действия;
– цель: действие посетителя сайта, которое считается наиболее ценным;
– конверсия: процентное соотношение числа посетителей, выполнивших целевое действие, к общему числу посетителей;
– источники трафика: каналы, откуда пришли посетители;
– возвраты: те случаи, когда пользователи добавили сайт к себе в закладки и заходят из них, либо пользователи, которые запомнили домен [2].
Представленные метрики классифицируются на 2 категории: количественные и качественные. Количественные показатели использовались для анализа временных тенденций и прогнозирования, качественные помогают классифицировать или сегментировать пользователей для анализа поведения конкретных групп. В рамках представленной задачи целевым показателем будет являться трафик, основной набор данных будет выглядеть как временной ряд количества посещений в единицу времени. В работах исследователей под временным рядом принято понимать последовательность наблюдений, записанных через последовательные временные интервалы. Данные временных рядов собираются через регулярные промежутки времени, например, ежечасно, ежедневно, ежемесячно, ежегодно [3–5]. Данные о трафике представляют собой временной ряд, что позволяет применять к ним различные методы прогнозирования – как статистические, так и методы машинного обучения.
Статистические методы работают с двумерными данными (количественная переменная, расположенная на временном отрезке), которые подаются на вход модели, что позволяет выделить как сезонную составляющую, так и трендовую. Однако не все данные подходят для таких методов. Для верификации пригодности временного ряда необходимо провести анализ стационарности ряда. Это фундаментальное свойство для многих моделей анализа временных рядов, при котором математическое ожидание, дисперсия и структура автоковариаций остаются постоянными во времени. Для проверки данного свойства ряда проводят тест Дики – Фуллера [6]:
yt = θyt – 1 + εt,
где yt – значение временного ряда в момент t; θ – коэффициент; εt – случайная ошибка.
Временной ряд является стационарным, а значит, не содержит единичный корень и описывается авторегрессионным процессом первого порядка, когда ∣θ∣ < 1. При θ = 1 временной ряд нестационарен, содержит единичный корень и описывается процессом случайного блуждания [6]. Несмотря на важность данного теста, его выполнение необязательно при применении методов машинного обучения. Напротив, данные методы широко используются для обнаружения сложных и непрямых связей внутри данных, но для этого необходимо большое количество feature-переменных. Под feature-переменной в работе [7] Орельена Жерона понимается отдельная измеряемая характеристика или свойство наблюдаемого явления. Другие качественные и количественные данные, помимо трафика, смогут выступить в роли дополнительных, описательных переменных, например общее количество просмотров, сеансов и событий. Также на основе количественных переменных можно рассчитать статистические feature-переменные, такие как лаги переменной, средние и медианные значения за различные периоды, отклонения и дельты. Кроме того, из самой даты необходимо собрать определенное количество переменных, важных для установления сезонной связи в модели.
Построение и сравнение моделей прогнозирования
Для анализа эффективности различных методов прогнозирования используется открытый источник данных: веб-трафик различных страниц Википедии. В работе разобраны методы SARIMA, Хольта – Винтера и градиентный бустинг. Перед работой с моделями необходимо провести анализ данных. В него входят общая визуализация данных, анализ наиболее значимых статей и STL-разложение. Временной ряд, представленный на графике (рис. 1), сильно подвержен сезонности.
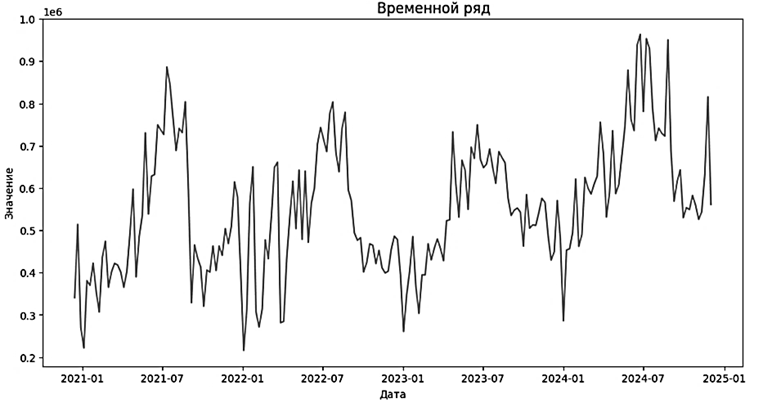
Рис. 1. Визуализация данных о посещении страниц Википедии
Fig. 1. Visualization of Wikipedia page visit data
Для дальнейшего анализа потребуется STL-разложение и анализ сезонной компоненты. Не менее значимым является выявление основных контрибуторов – самых объемных по посещаемости страниц, т. к. они наиболее сильно будут влиять на оценку моделей (рис. 2).
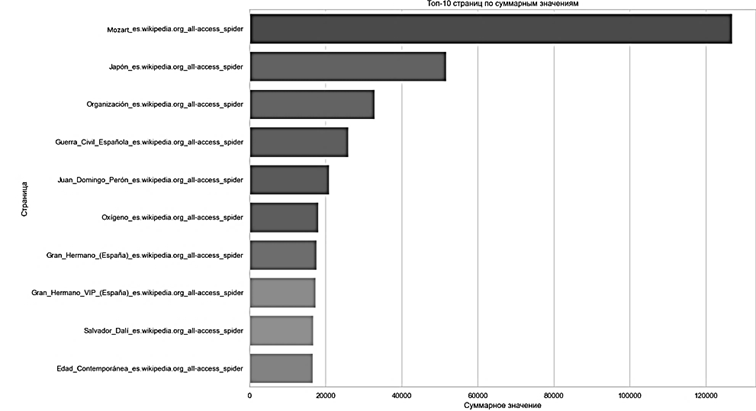
Рис. 2. Топ-10 страниц по посещению
Fig. 2. Top-10 pages by visits
Как видно на графике, статья Википедии, посвященная Моцарту, является наиболее популярной, следовательно, для моделей SARIMA и Хольта – Винтера будет иметь большое значение стационарность этого ряда.
Разложим данные на компоненты STL: сезонность, тренд и потери (рис. 3).
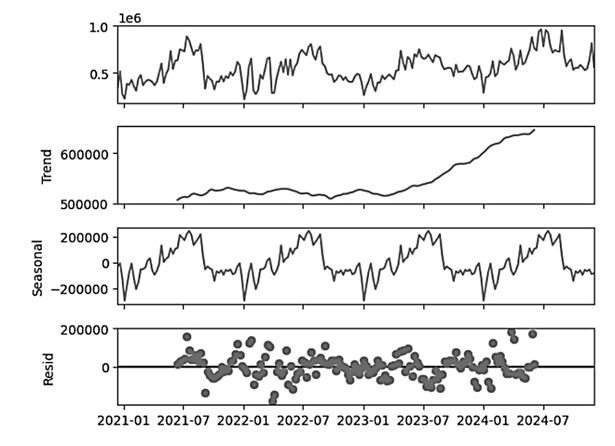
Рис. 3. STL-разложение временного ряда
Fig. 3. STL decomposition of time series
Исходя из STL-разложения, можно сделать вывод о повышении популярности Википедии, а также сильной сезонности, которая может объясняться сезонностью в сфере образования: экзамены, сессии. Приступим к построению прогнозных моделей, т. к. SARIMA работает исключительно с двумерными рядами, просчет модели будет происходить в итеративном формате, по каждому ряду по отдельности. Предварительно данные были сгруппированы по неделям для прогнозирования на более высоком уровне. Максимально возможный период прогнозирования зависит от исторического периода данных и может составлять четверть от исторического периода. Для данных о веб-трафике различных страниц Википедии период составляет 13 недель. Сама модель SARIMA использует несколько статистических показателей для прогноза: S – сезонность, AR – авторегрессия, I – интеграция, MA – скользящее среднее. На вход модель принимает 7 параметров: порядки каждой составляющей, сезонные порядки каждой составляющей и период сезонности, в прогнозировании по неделям период равен 52. В данной работе был проведен анализ наиболее подходящих параметров каждой переменной от 0 до 5 с шагом 1. Лучшая модель для каждого ряда далее выступала как результирующая для получения наибольшей точности. Результат представлен на рис. 4.
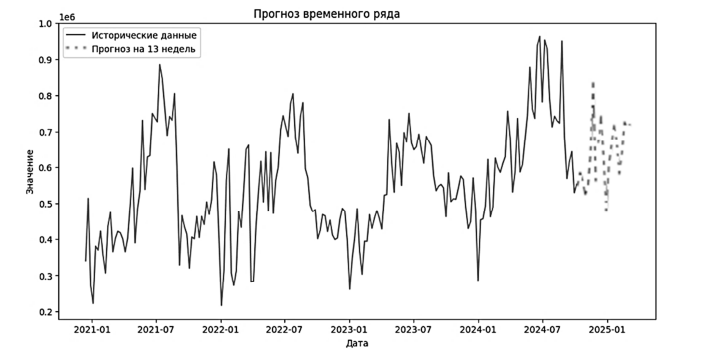
Рис. 4. Прогноз модели SARIMA
Fig. 4. SARIMA model forecast
Далее исследуется модель Хольта – Винтера, за основу которой взято разложение ряда на сезонную и трендовую составляющие. Такое разложение комбинируется с экспоненциальным сглаживанием, что лишает ее определенной гибкости. Данная модель подходит для стабильных рядов, с одинаковой сезонностью и понятным трендом. Ряды посещений Википедии сложно назвать стабильными, т. к. тренд в отдельно взятых рядах нестабилен. Результат прогноза адаптивной модели Хольта – Винтера представлен на рис. 5.

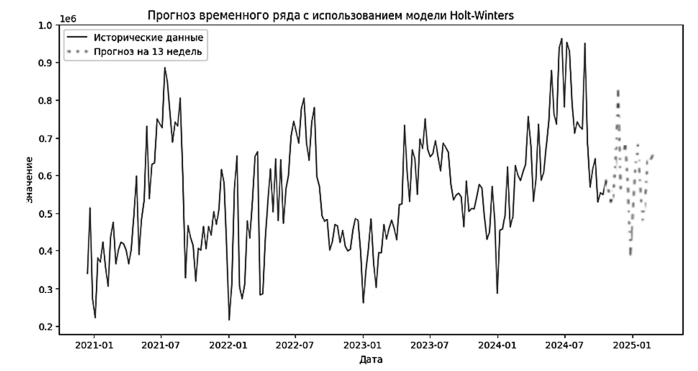
Рис. 5. Прогноз адаптивной модели Хольта-Винтера
Fig. 5. Holt–Winters adaptive model prediction
Далее рассмотрим более сложную модель, которая уже может включать в себя дополнительные feature-переменные – градиентный бустинг. Принцип работы заключается в постепенном итеративном наращивании более слабых моделей для получения точного прогноза. Свое название метод получил благодаря использованию принципа градиентного спуска, где на каждой итерации считается градиент функции потерь, последующие модели обучаются на нем, улучшаясь в нужном направлении. Ключевым фактором успешного применения градиентного бустинга является использование корректных feature-переменных. Из полученных данных удалось создать 24 статистических переменных: 13 лагов переменной, среднее, медиана, стандартное отклонение за 4, 8 и 13 недель, дельты первого лага и среднего, медианы. Также 5 временных переменных, описывающих год, месяц, номер недели, сезон и квартал. Наиболее важными по итогу прогнозирования оказались месяц, первый лаг, среднее за 4 недели. Результат представлен на рис. 6.
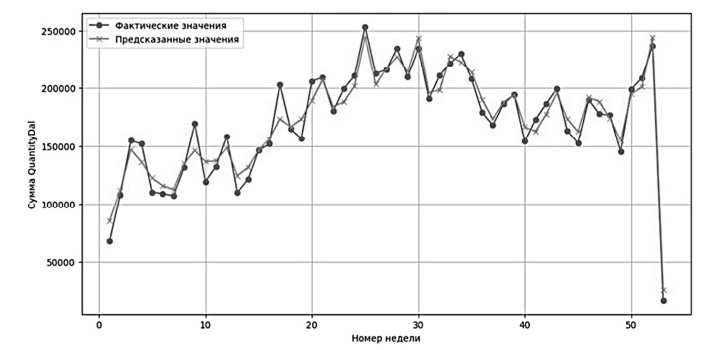
Рис. 6. Прогноз модели градиентного бустинга
Fig. 6. Prediction of the gradient boosting model
Для анализа точности моделей использовались 3 метрики: MSE, MAE и RMSE. MSE – среднеквадратичное отклонение, рассчитывает, насколько предсказанное значение отклоняется от фактических. Однако у MSE есть недостаток: т. к. он считается в квадрате, его интерпретация может вызывать осложнения. Для более легкой интерпретации в работе используется параметр RMSE, который берет корень от MSE. В качестве третьего параметра используется MAE – средняя абсолютная ошибка, которую можно интерпретировать как модуль дельты фактического и предсказанного значения. Результаты сравнения моделей представлены на рис. 7.
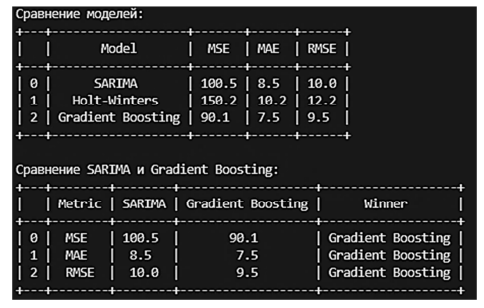
Рис. 7. Сравнение моделей по прогнозированию посещений Википедии
Fig. 7. Comparison of models for predicting visits Wikipedia
На основании полученных значений метрик можно сделать вывод, что модель градиентного бустинга продемонстрировала наименьшую ошибку прогноза в задаче прогнозирования посещаемости страниц Википедии.
Заключение
Научная новизна работы заключается в комплексном подходе к прогнозированию посещаемости веб-ресурсов, сочетающем традиционные и современные методы, а также в практических выводах, которые могут быть полезны для бизнеса и дальнейших исследований в этой области. Несмотря на то, что модель градиентного бустинга продемонстрировала наилучшие результаты, для некоторых рядов более точной оказалась модель SARIMA, для некоторых – Хольта – Винтера. Полученные результаты свидетельствуют о необходимости комбинации различных методов для достижения наиболее точного прогноза. Также следует рассмотреть возможность ансамблирования моделей в разных пропорциях. Задача прогнозирования посещаемости веб-ресурсов стала одной из ключевых задач маркетинга и интернет-торговли. Поскольку данная сфера с каждым годом набирает популярность, важность подобных моделей для бизнеса будет расти, а методы становиться более сложными и точными. Кроме того, следует обратить внимание на использование рекуррентных искусственных нейронных сетей для прогнозирования посещаемости. Применение моделей, которые обладают способностью учитывать временные зависимости и сложные паттерны в данных, потенциально повышает точность прогнозирования.
Таким образом, будущее прогнозирования посещаемости веб-ресурсов связано с интеграцией различных методов и технологий, что позволит бизнесу не только адаптироваться к изменениям на рынке, но и предвосхищать потребности своих клиентов. Важно продолжать исследовать и внедрять новые подходы, чтобы оставаться на шаг впереди в этой быстро меняющейся среде.
1. Internet-torgovlya (rynok Rossii) [Online commerce (Russian market)]. TADVISER. Gosudarstvo. Biznes. Tekhnologii. Available at: https://clck.ru/3RGv9z (accessed: 09.04.2025).
2. Knaan A. R. Ispol'zovanie instrumentov veb-analitiki dlya uluchsheniya poseshchaemosti sajta [Using web analytics tools to improve website traffic]. Nauchnyj rezul'tat. Informacionnye tekhnologii, 2020, vol. 5, no. 2, pp. 32-37.
3. Hajndman R. D., Atanasopulos Dzh. Prognozirovanie: principy i praktiki [Forecasting: principles and practices]. Moscow, DMK Press, 2023. 458 p.
4. Surina A. V. Analiz vremennyh ryadov: uchebnoe posobie [Time series analysis: a textbook]. Saint Petersburg, 2025. 90 p.
5. Shamvej R. H., Stoffer D. S. Analiz vremennyh ryadov i ego prilozheniya [Time series analysis and its applications]. Springer, 2017. 562 p.
6. Test Diki – Fullera [The Dickey–Fuller Test]. Available at: https://bigenc.ru/c/test-diki-fullera-ba2fa5 (accessed: 09.04.2025).
7. Géron A. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow. O'Reilly Media, Inc., 2022. 864 p.