Saratov, Russian Federation
Saratov, Russian Federation
UDC 004.4
UDC 004.421
UDC 519.685
The development of artificial intelligent systems usually requires a huge investment of time and effort from the developer to provide them with a small fraction of the capabilities of biological prototypes. Building knowledge models of intelligent systems is the most complex and time-consuming process. The application of biological systems principles is intended to accelerate progress in this direction. Biological systems have effective learning and, most importantly, self-learning abilities with the formation of skills and abilities, the rapid application of which helps them survive in an aggressive environment. Neural network mechanisms of memory and decision-making are capable of self-organization, rebuilding neural structures based on the accumulation of knowledge in changing environmental conditions. The organization of memory based on an adaptive neuron, capable of independently adjusting the ratio between various combinations of various signals coming to the inputs and signals of different shapes and levels at the output, allows even one element of the neural structure of the brain to store large amounts of relatively “simple” information. When interacting with other neurons, structural relationships are established between combinations of elementary information, forming experience, skills, and abilities, the generalization of which leads to the emergence of knowledge. Providing artificial intelligent systems with self-learning abilities should qualitatively change the process of their construction. An approach to improving self-organizing control systems based on the principles of biological systems, multilevel memory, mechanisms of structuring and generalization is proposed. The simplest example of the implementation of these principles is the use of plans for solving “simple” tasks as components of plans for solving more complex tasks. The use of structuring, generalization, and axiomatization of solutions to known problems allows you to create new knowledge that can then be used to solve new problems. An algorithm for solving problems based on the use of multilevel memory, structuring, generalization and axiomatization of procedural knowledge is proposed. An example of solving a declarative set task using self-learning is considered, demonstrating the effectiveness of the proposed approach.
self-learning, self-organization, action planning, multilevel knowledge representation, intellectual systems, automatic problem solving
Введение
Создание интеллектуальных систем обусловлено необходимостью обеспечения эффективного функционирования в столь сложных, изменяющихся условиях, когда автоматические системы, разрабатываемые традиционными методами, не могут обеспечить требуемые показатели точности и качества [1]. Однако возможности современных систем, относимых к интеллектуальным, ограничены и определяются не только формализованными описаниями окружающего мира, которые называют не вполне заслуженно знаниями, но и методами, заложенными разработчиком для их обработки в процессе решения поставленных задач [1]. Искусственные интеллектуальные системы (ИИС), построенные на основе искусственной нейронной сети, обычно решают задачи классификации, распознавания, аппроксимации [2, 3], что обеспечивается предварительным длительным обучением различными методами [4–6] на больших множествах примеров. При этом ИИС, построенные на основе формальных логических систем, сетевых моделей представления знаний [1], позволяют решать задачи в рамках имеющейся модели знаний [7]. Как следствие, современные ИИС способны решать задачи предопределенного класса в рамках имеющейся модели мира [8, 9]. При этом и постановка задачи должна строго соответствовать установленным правилам, шаблонам, заданным разработчиком. Появление задач других классов или в другой форме приводит к большим ошибкам или к отказу от решения.
«Живые» примеры биологических систем демонстрируют поразительные способности решения задач различных классов в различных формах представления. Этому, по-видимому, способствует использование нейросетевых структур мозга биологических систем, способных устанавливать новые связи между нейронами при наличии выявляемых взаимосвязей между определенными понятиями (сущностями, образами, фактами) в окружающем фактическом или гипотетически построенном виртуальном мире.
Организация памяти на основе адаптивного нейрона, способного самостоятельно подстраивать соотношение между различными комбинациями различных сигналов, поступающих на входы, и различными по форме и уровню сигналами на выходе, позволяет даже в одном элементе нейронной структуры мозга запоминать большие объемы относительно «простой» элементарной информации. Благодаря наличию взаимодействия как с соседними, так и с другими нейронами реализуются механизмы установления взаимосвязей между различными комбинациями элементарной информации, что создает информационные структуры (структурированное представление информации). Так формируются опыт, навыки, умения, а результат их обобщения приводит к появлению знаний.
Примером формализации указанных принципов может служить обучение Хэбба [10–13]. При этом биологические системы применяют эффективные механизмы (процедуры) решения как типовых, так и новых задач. Основу этих механизмов составляют [14–16] планирование действий, моделирование их выполнения, сопоставление результатов моделирования с требуемыми результатами, принятие полученного решения или построение новой программы действий [7]. Успешно решенная задача приводит к установлению новых связей между нейронами, представляющими задачи, и нейронами, представляющими действия по их решению. Так формируются новые знания, способствующие интеллектуальной системе адаптироваться в изменчивой внешней среде. Преимущество способностей биологических систем обусловлено использованием многоуровневых представлений знаний, в которых данные и операции, задачи и цели размещены на различных уровнях разных «подмоделей знаний», представляемых различными нейронными ансамблями (нейронными алгоритмическими структурами). Указанный способ организации нейросетевых структур решения задач позволяет биологическим системам при решении каждой конкретной задачи осуществлять поиск решения в рамках конкретной модели знаний обозримого объема, получая решение за разумное время, достаточное для принятия адекватного решения в агрессивной внешней среде [17]. Таким образом, формируемая биологическими системами нейросетевая модель окружающего мира, в котором им приходится решать задачи, непрерывно совершенствуется, что позволяет расширять классы решаемых задач по мере их возникновения. Подобные системы принято называть самоорганизующимися [1]. Вычислительная сложность методов решения декларативно поставленных задач ИИС обусловливает необходимость проведения исследований для повышения их эффективности, создания подходов, основанных на новых принципах. Указанные способности различной степени глубины демонстрируют биологические системы различной степени сложности своей организации, что позволяет говорить о наличии всеобщих для всех биологических систем принципов построения систем решения задач. Среди этих принципов, по-видимому, одним из важнейших, обеспечивающих формирование, накопление и корректировку знаний, является принцип самообучения на основе многоуровневой организации памяти, создающей условия для масштабирования функциональных возможностей по объемам накапливаемых структурированных знаний и адекватных механизмов их обработки для решения задач за время, позволяющее биологическим системам принимать разумные решения выживания в агрессивной окружающей среде.
Цель исследования заключается в разработке подхода к созданию системы автоматического решения задач, обладающей способностями к самоорганизации на основе самообучения, обеспечивающими возможности автоматической настройки на обобщенные классы задач посредством использования многоуровневой организации памяти, автоматического формирования и корректировки взаимосвязанных компонентов многоуровневого представления знаний.
Задача исследования заключается в разработке алгоритма самообучения решателя задач интеллектуальной системы, использующего принципы самоорганизации биологических систем на основе использования многоуровневых моделей представления знаний интеллектуальных систем для обеспечения возможности решения новых непроцедурно (декларативно) поставленных задач на основе знаний о методах проблемной области.
Метод самоорганизации нейросетевого решателя на основе самообучения
Изложение предлагаемого подхода и его исследование осуществим на примере предметной области построения интеллектуальных систем автоматического управления [18, 19]. Отличительной особенностью предлагаемого подхода к самообучению, самоорганизации интеллектуального решателя задач [20] является использование иерархически связанных планирующих искусственных нейронных сетей (ПИНС) [15, 16], перестраиваемых в соответствии с изменениями модели знаний, осуществляемыми в процессе самоорганизации в результате самообучения в соответствии с принципами работы биологических систем.
Алгоритм самообучения предлагаемого подхода к самоорганизации решателя задач осуществляет формирование алгоритмических конструкций многоуровневого представления знаний ИИС:
– «опыт» в виде построенного плана решения задачи, сохраняемого в кратковременной (оперативной) памяти. Действенность указанного опыта подтверждена при решении задачи применением плана (программы) ее решения;
– «умение» как аксиоматизированный «опыт», формируемый созданием аксиом модели знаний с атрибутами ранее неоднократно решенной задачи и сохраняемый в долговременной памяти. Указанные аксиомы новых «умений» дополняют модель знаний ИИС после проверки на непротиворечивость. Затем модифицированная модель знаний используется для корректировки (перестройки) нейросетевых структур решателя задач.
Таким образом, предлагаемый подход к самообучению нейросетевого решателя задач, заключающийся в корректировке формализованной модели знаний ИИС, представляет собой возможный механизм самоорганизации ИИС, основанный на обобщении накопленного в кратковременной памяти «опыта» решения задач в аксиоматизированные в долговременной памяти «умения» многоуровневого нейросетевого представления знаний, что, возможно, соответствует механизмам самообучения биологических систем.
Алгоритм самообучения решателя задач
1. Определение цели системы (целеполагание) G(t) = OG(S(t), F(t)), где G(t) – цель; t – время; OG(×) – операция целеполагания; S(t) – состояние системы; F(t) – внешние воздействия.
2. Постановка задачи Z = < GZ, PZ, DZ, RZ, TZ > = OZ (G(t), S(t), F(t)), где GZ – цель решения задачи как обобщенный искомый результат; PZ – план решения задачи; DZ – исходные данные задачи; RZ – искомый результат решения задачи; TZ – требования к искомому результату решения задачи; OZ(×) – операция формирования постановки задачи. Если Z = Æ, то идти к п. 1.
3. Распределение (декомпозиция) задачи Z на множество подзадач Zi = {zij} по подсистемам Ai (агентам) Zi = Z(Ai) = {zij} = OD (Z(t), Mi(t), G(t), S(t), F(t)), "iÎ(1, nA), "jÎ(1, ni), где OD – операция декомпозиции; zij – j-я подзадача множества задач Zi, поставленных перед подсистемой (агентом) Ai ИИС; Mi – знания (модель знаний) подсистемы Ai; nA – количество подсистем; ni – количество задач i-й подсистемы. Если ÈZi = Æ, то отказ (задача Z помечается «нерешаемой»), идти к п. 2.
4. Построение агентами Ai планов действий для решения задач Zi: P(Zi) = {P(zij)} = OP (Zi, Mi, Z, G), "iÎ(1, nA) процедурой планирования OP .
5. Моделирование выполнения на моделях знаний Mi агентами Ai множества планов P(Zi) решения множества задач Zi ={zij} на основе процедуры OM моделирования "i Î(1, nA), "jÎ(1, ni) < GijM (zij), RijM (zij) > = OM (P(zij), Mi, S(t), F(t)), RiM (Zi) = È RijM (zij), GiM (Zi) = È GijM (zij), где индекс XM является признаком, что результат Х является модельным (гипотетическим), т. к. получен посредством моделирования исполнения плана решения задачи.
6. Оценка возможности достижения целей решения поставленных задач eijM = T(zij) = r(< GijM (zij), RijM (zij) >, < Gi(zij), Ri(zij) >), eiM = supj(eijM), где r(x, y) – мера близости x и y.
Если eiM £ ei, где ei – допустимое значение погрешности (ошибки) решения задач Zi, то сохранение в «оперативной памяти» решения задач zij "jÎ(1, ni) как «опыт» в виде, применяемом при записи продукционных правил: < имя аксиомы (правила) > : < условия применимости > → < исходные данные > Þ < искомый результат > ¬ < требования к искомому результату >: Azij : C(zij) ® D(zij), S(t), F(t) Þ R(zij), G(zij) ¬ T(zij), где D(zij) Í Í D(Z), R(zij) Í R(Z), G(zij) Í G(Z), T(zij) Í T(Z), где Azij – имя создаваемой в оперативной (кратковременной памяти) аксиомы, описывающей успешный «опыт» решения задачи zij; D(zij) – исходные данные задачи zij, R(zij) – искомый результат, C(zij) – условия применимости аксиомы и T(zij) – требования к искомым результатам задачи, которые могут отсутствовать. Идти к п. 7.
Иначе блокирование решения задачи zij, не обеспечивающей достижение требований T(zij) в виде создаваемой в оперативной (кратковременной памяти) аксиомы, описывающей негативный «опыт» решения задачи zij, Azij: C(zij) ® D(zij), S(t), F(t) Þ R(zij), G(zij) ¬ ~T(zij), где «~» – символ отрицания (логическое НЕ). Идти к п. 3.
7. Исполнение планов P(Zi) решения задач
Zi = {zij} "iÎ(1, nA), "jÎ(1, ni) < GijР(zij), RijР(zij) > = = OИ(P(zij), Mi, S(t), F(t)), RiР(Zi) = È RijР(zij), GiР(Zi) = = È GijР(zij), где индекс XР является признаком, что результат Х является полученным в процессе реального (фактического) исполнения агентом Ai плана действий P(zij) решения задачи zij.
8. Оценка достижения целей решения задач Zi = {zij} "iÎ(1, nA), "jÎ(1, ni) eijР = r(< GijР(zij), RijР(zij) >, < Gi(zij), Ri(zij) >), eiР = supj(eijP), e = supi(eiP).
Если eiР < ei, то преобразование «опыта» в «умения» (перенос аксиом в «долговременную память»).
Иначе идти к п. 2.
9. Оценка достижения глобальной цели. Если
e < e, то формирование аксиомы Az: C(Z) ® D(Z), S(t), F(t) Þ R(Z), G(Z) ¬ T(Z). Конец.
Иначе идти к п. 1.
Основная идея предлагаемого подхода к самоорганизации c использованием многоуровневой памяти, включающей кратковременную память «опыта решения задач» и долговременную память «умений ранее неоднократно решенных задач» в ИИС может быть проиллюстрирована на модельном примере планирования действий при решении новых задач при наличии обобщенного (аксиоматизированного) в «умения» ранее полученного «опыта» решения задач.
Решение модельного примера
Рассмотрим пример самообучения подсистемы Ai решателя задач ИИС на основе опыта решения задач. Для описания примера введем следующие обозначения: Д – действие (операция), О – отношение, С – свойство, Х – характеристика, Ф – форма математической модели, & – конъюнкция (логическое И), «~» – отрицание (логическое НЕ).
Формат текстового описания задач и действий модели знаний (выражение в квадратных скобках [x] является необязательным, т. е. может отсутствовать).
Формат описания задачи на модели знаний:
<Данные> ® <Результат> [¬ <Требования к результату>]
Формат описания действия (аксиомы) модели знаний Mi подсистемы Ai:
<Имя действия>: [<Условия>] ® <Данные> Þ <Результат> [¬ <Требования к результату>]
Аксиоматика модели знаний Mi рассматриваемого примера:
Д1: ® Ф1, Ф2 Þ С1
Д2: ® Ф1, Ф2, Ф5 Þ С2
Д3: ® Ф1, Ф2 Þ С3
Д4: ~С2 ® Ф1, Ф5 Þ Х1
Д5: С1&С2 ® Ф4, Ф5 Þ Ф3
Д6: ~С1&С2 ® Ф4, Ф5 Þ Ф3
Д7: С1&~С2 ® Х1, Ф4, Ф5 Þ Ф3
Д8: ~С1&~С2 ® Х1, Ф4, Ф5 Þ Ф3
Д9: С3® Ф1, Ф2 Þ Ф5
Д10: ® Ф1, Ф2, Ф5 Þ Ф4 ¬ О2
Д11: ® Ф1, Ф2, Ф3 Þ О1
Д12: ® Ф1, Ф2, Ф4, Ф5 Þ О2
Задача 1 (Z1):
Z1: Ф1, Ф2 ® Ф3 ¬ О1
Задача 2 (Z2):
Z2: Ф1, Ф2 ® Ф4, Ф5 ¬ О2
Решение задачи 1 (план P(Z1) из 12 действий как множество действий, описываемых аксиомами модели знаний, подлежащих выполнению для решения задачи 1):
Д1: ® Ф1, Ф2 Þ С1
Д3: ® Ф1, Ф2 Þ С3
Д9: С3 ® Ф1, Ф2 Þ Ф5
Д10: ® Ф1, Ф2, Ф5 Þ Ф4 ¬ О2
Д12: ® Ф1, Ф2, Ф4, Ф5 Þ О2
Д2: ®Ф1, Ф2, Ф5 Þ С2
Д4: ~С2 ® Ф1, Ф5 Þ Х1
Д5: С1&С2® Ф4, Ф5 Þ Ф3
Д6: ~С1&С2® Ф4, Ф5 Þ Ф3
Д7: С1&~С2® Х1, Ф4, Ф5 Þ Ф3
Д8: С1&~С2® Х1, Ф4, Ф5 Þ Ф3
Д11: ® Ф1, Ф2, Ф3 Þ О1
Решение задачи 2 (Z2) (план P(Z2) из 4 действий):
Д3: ®Ф1, Ф2 Þ С3
Д9: С3® Ф1, Ф2 Þ Ф5
Д10: ®Ф1, Ф2, Ф5 Þ Ф4 ¬ О2
Д12: ®Ф1, Ф2, Ф4, Ф5 Þ О2
Обобщим решение задачи 2 (Z2) в «опыт», а затем в «умение» в виде действия (аксиомы):
Д13: ® Ф1, Ф2 Þ Ф4, Ф5 ¬ О2
План решения задачи 1 (Z1) с учетом умения Д13 включает 9 действий и дает дополнительно экономию времени решения (планирования действий) в 30 %:
Д1: ® Ф1, Ф2 Þ С1
Д13: ® Ф1, Ф2 Þ Ф4, Ф5 ¬ О2
Д2: ® Ф1, Ф2, Ф5 Þ С2
Д4: ~С2® Ф1, Ф5 Þ Х1
Д5: С1&С2® Ф4, Ф5 Þ Ф3
Д6: ~С1&С2® Ф4, Ф5 Þ Ф3
Д7: С1&~С2® Х1, Ф4, Ф5 Þ Ф3
Д8: ~С1&~С2® Х1, Ф4, Ф5 Þ Ф3
Д11: ® Ф1, Ф2, Ф3 Þ О1
Результаты и обсуждение
Модельный пример решен в системе автоматического решения задач ИНСТРУМЕНТ-4, являющейся дальнейшим развитием системы ИНСТРУМЕНТ-3м-И [15], которая обладает нейросетевым решателем задач на основе ПИНС и разрабатывалась для автоматизации решения задач построения законов (алгоритмов) управления систем автоматического управления.
Система ИНСТРУМЕНТ-4 представляет собой распределенную мультиагентную информационную систему, в которой подсистемы планирования действий, исполнения планов решения задач, баз данных и знаний реализованы в виде отдельных серверных приложений, а пользовательский интерфейс представлен в виде клиентского приложения.
Для обеспечения возможности решения декларативно поставленных задач в составе системы ИНСТРУМЕНТ-4 имеется база знаний, в которой базовая модель знаний ориентирована на автоматическое решение задач проектирования линейных непрерывных и дискретных алгоритмов управления объектами управления, описываемыми линейными обыкновенными дифференциальными уравнениями, а также моделирования замкнутой системы с учетом наличия нелинейностей, нестационарности и параметрической неопределенности объекта управления. Система ИНСТРУМЕНТ-4 предоставляет инженерам-проектировщикам систем управления в пользовательском интерфейсе «Среда инженера» возможности автоматического решения задач в декларативной постановке на основе моделей знаний, разрабатываемых учеными-исследователями. Работа со знаниями реализована в пользовательском интерфейсе «Среда исследователя», которая предоставляет ученым-исследователям возможности создания моделей знаний и их тестирования на модельных задачах. Для обеспечения возможности использования инженерами-проектировщиками моделей знаний, разработанных учеными-исследователями, в «Среде исследователя» предусмотрена возможность задания реализации действий, описываемых аксиомами моделей знаний. Указанная реализация действий осуществляется в виде программного модуля на языке С++, оформляемого по предлагаемому шаблону и размещаемого в библиотеке динамической загрузки инженером-программистом под руководством ученого-исследователя. Поскольку в сообществе ученых-исследователей (специалистов в области автоматического управления) популярно использование пакета Matlab, то в системе ИНСТРУМЕНТ-4 допускается также использование реализации действий, описываемых аксиомами моделей знаний в виде программ на Matlab-подобном языке, что позволяет ученым-исследователям самостоятельно без привлечения инженеров-программистов расширять классы решаемых задач.
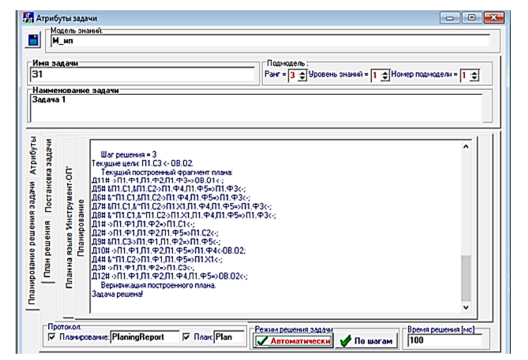
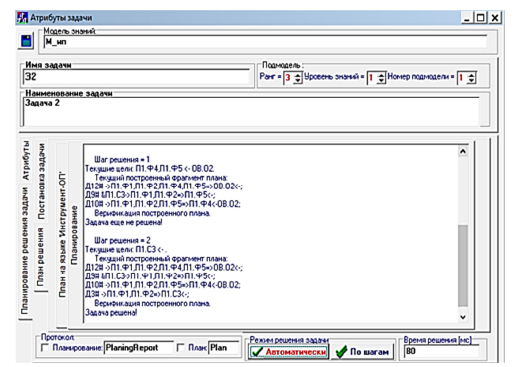
На рис. 1, 2 представлены изображения экранных форм «Среды исследователя», иллюстрирующие решение задач 1 и 2, а также решение задачи 1 с учетом дополнительного действия Д13, представляющего собой «умение», аксиоматизированное на основе «опыта» решения задачи 2, протокол решения указанных задач представлен на вкладке «Планирование» экранной формы «Среды исследователя».
а
б
Рис. 1. Протокол решения задач: а – задачи 1; б – задачи 2
Fig. 1. Task solution protocol: а – tasks 1; б – tasks 2
а
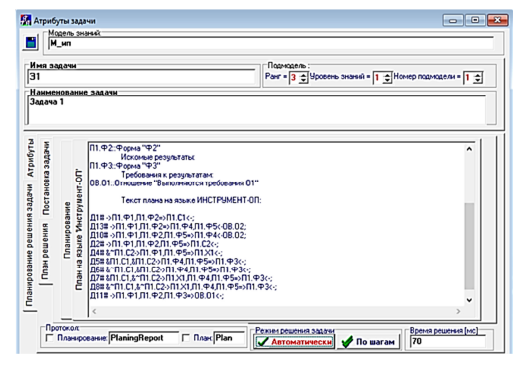
б
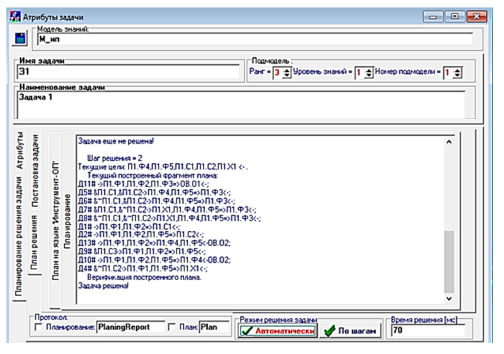
Рис. 2. Протокол решения задачи 1 на скорректированной модели знаний:
а – протокол планирования действий; б – построенный план решения задачи
Fig. 2. Protocol for solving problem 1 based on the adjusted knowledge model:
а – protocol for planning actions; б – a constructed plan for solving the problem
Показана эффективность предлагаемого подхода к обучению планирующей подсистемы решателя задач на примере решения модельной задачи. Экономия времени решения задачи после самообучения составила 30 % (результат сопоставления – см. рис. 1 и 2: 100 мс и 70 мс).
Заключение
Способности запоминать, накапливать опыт и умения позволяют биологическим системам обеспечить выживаемость во враждебной среде обитания. Самоорганизация технических систем нацелена на обеспечение возможностей достижения целей не только в нормальных, но и в экстремальных условиях. Использование самообучения, иерархических механизмов памяти повышает эффективность самоорганизации. Разработанный алгоритм решения задач самоорганизующейся системой управления включает самообучение подсистемы планирования действий. Эффективность предлагаемого подхода демонстрируется решением модельной задачи на модели знаний в системе автоматизации решения задач. Дальнейшие исследования посвящены развитию предложенного подхода в направлении автоматического решения декларативно поставленных задач итерационными методами, что требует способности порождения циклически выполняемых планов действий.
1. Iskusstvennyj intellekt: spravochnik: v 3-kh knigah [Artificial Intelligence: a reference book]. Pod redakciej D. A. Pospelova. Moscow, Radio i svyaz' Publ., 1990. Book 1. 464 p. Book 2. 304 p. Book 3. 368 p.
2. O’Reilly R., Munakata Y., Frank M. J., Hazy T. E. Computational Cognitive Neuroscience. Online Book. Available at: https://www.researchgate.net/profile/Randall-Oreilly/publication/233822187_Computational_Exploration_in_Cognitive_Neuroscience/links/606e18dd92851c8a7baf2f98/Computational-Exploration-in-Cognitive-Neuroscience.pdf (accessed: 12.06.2025).
3. Hassabis D., Kumaran D., Summerfield C., Botvinic M. Neuroscience-Inspired Artificial Intelligence. Neuron, 2017, vol. 95, no. 2, pp. 245-258. DOI:https://doi.org/10.1016/j.neuron.2017.06.011.
4. Botteghi N. Robotics deep reinforcement learning with loose prior knowledge. Enschede, University of Twente, 2021. 239 p.
5. Goodfellow I., Bengio Y., Courville A. Deep learning. MIT Press, 2016. Vol. 1. 800 p.
6. Pateria S., Subagdja B., Tan A., Quek C. Hierarchical Reinforcement Learning: A Comprehensive Survey. ACM Computing Surveys, 2021, vol. 54 (5), pp. 1-35. DOI:https://doi.org/10.1145/3453160.
7. Anohin P. K. Principial'nye voprosy obshchej teorii funkcional'nyh sistem [Fundamental issues of the general theory of functional systems]. Principy sistemnoj organizacii funkcij. Moscow, Nauka Publ., 1973. Pp. 5-61.
8. Hafner D., Pasukonis J., Ba J., Lillicrap T. Mastering diverse domains through world models. arXiv preprint arXiv:2301.04104, 2023. Available at: https://arxiv.org/abs/2301.04104 (accessed: 12.06.2025).
9. Dzhivelikian E., Latyshev A., Kuderov P., Panov A. Hierarchical intrinsically motivated agent planning behavior with dreaming in grid environments. Brain Informatics, 2022, vol. 9, no. 1, p. 8. Available at: https://doi.org/10.1186/s40708-022- 00156-6 (accessed: 12.06.2025).
10. Hebb D. O. The organization of behavior: A neuropsychological theory. Psychology press, 2005. 279 p.
11. Amato G., Carrara F., Falchi F., Gennaro C., Lagani G. Hebbian Learning Meets Deep Convolutional Neural Networks. Image Analysis and Processing – ICIAP 2019: 20th International Conference (Trento, Italy, September 9–13, 2019), Proceedings, Part I. Cham, Springer International Publishing, 2019. Pp. 324-334.
12. Moraitis T., Toichkin D., Journé A., Chua Y., Guo Q. Softhebb: Bayesian inference in unsupervised hebbian soft winner-take-all networks. Neuromorphic Computing and Engineering, 2022, vol. 2, no. 4, p. 044017.
13. Journ´e A., Rodriguez H. G., Guo Q., Moraitis T. Hebbian deep learning without feedback. arXiv preprint arXiv:2209.11883, 2022. Available at: https://arxiv.org/pdf/2209.11883 (accessed: 12.06.2025).
14. Efimov E. I. Reshateli intellektual'nyh zadach [Intellectual Problem Solvers]. Moscow, Nauka Publ. 1982. 316 p.
15. Stepanov M. F. Nejronnye seti dlya planirovaniya resheniya zadach teorii avtomaticheskogo upravleniya [Neural networks for planning solutions to problems in the theory of automatic control]. Problemy upravleniya, 2004, no. 2, pp. 66-71.
16. Stepanov M. F., Stepanov A. M., Stepanova T. V., Stepanova O. M. Features of Knowledge Representation of Automatic Control Systems Design Methods. International Conference Artificial Intelligence in Engineering and Sci-ence (Studies in Systems, Decision and Control). Springer Nature Switzerland AG, 2023. Vol. 457. Pp. 231-243. DOI:https://doi.org/10.1007/978-3-031-22938-1_16.
17. Stepanov M. F., Stepanov A. M., Stepanova O. M. Camoobuchenie nejrosetevogo reshatelya zadach intel-lektual'noj sistemy avtomaticheskogo upravleniya na osnove modelirovaniya samoobucheniya mozga [Self-learning of a neural net-work problem solver of an intelligent automatic control system based on modeling of self-learning of the brain]. Imperativ akademika A. A. Uhtomskogo – mozg i ego samopoznanie: tezisy dokladov i materialy Vserossijskoj nauchnoj konferencii (Sankt-Peterburg, 15–18 aprelya 2025 g.). Saint Petersburg, Izd-vo SPbGUPTD, 2025. Pp. 171-172.
18. Spravochnik po teorii avtomaticheskogo upravleniya [Handbook on the theory of automatic control]. Pod redakciej A. A. Krasovskogo. Moscow, Nauka Publ., 1987. 712 p.
19. Anohin P. K. Filosofskie aspekty teorii funkcion-al'noj sistemy [Philosophical aspects of functional system theory]. Moscow, Nauka Publ., 1978. 400 p.
20. Stepanov M. F., Stepanov A. M. Mathematical modelling of intellectual self-organizing automatic control system: Action planning research. Procedia Engineering, 2017, vol. 201, pp. 617-622.