Russian Federation
Astrakhan, Russian Federation
This paper examines the relevance of energy consumption forecasting and provides an analysis and comparison of different approaches used in this field. It describes the structure of the wholesale electricity and capacity mar-ket and the trading process, highlighting the advantages of wholesale trading for both buyers and sellers and explaining why accurate energy consumption forecasting is important under these market conditions. The research aim is defined as improving forecasting accuracy by developing and comparing models based on approaches ranging from classical statistical methods to modern machine learning and deep learning algorithms. Three main groups of methods are considered: statistical models (SARIMA); machine learning techniques (RF, XGBoost, SVM, k-NN, DT, AD); and deep learning models (LSTM, GRU, CNN, ResNet, Transformer). The paper also discusses model stacking, which allows combining outputs of different algorithms to increase forecast accuracy, and analyzes how combining multiple models affects the final results. Open hourly energy consumption data were used as the dataset, and numerical results were evaluated with MSE, RMSE, MAE, and MAPE metrics. The testing results highlight the strengths and weaknesses of methods from each group, provide a comparative analysis of the algorithms, and offer recommendations for improving the developed models. It is shown that the combined LSTM-GRU model achieves the best forecasting accuracy with a minimum MAPE of 1.86%. In addition, the performance of the Transformer model was improved from 2.8% to 2.25%, indicating the potential for further development of models within this architecture. The results confirm the effectiveness of hybrid neural network architectures for short-term energy consumption forecasting in power systems.
machine learning, electricity consumption forecasting, deep learning, time series, statistical models, LSTM
Введение
Современное развитие электроэнергетики Российской Федерации характеризуется ростом объемов потребления и усложнением структуры энергорынков. На оптовом рынке электроэнергии и мощности (ОРЭМ), функционирующем с 2006 г., взаимодействуют генерирующие, сетевые и сбытовые компании, деятельность которых регламентируется Федеральным законом № 35-ФЗ «Об электроэнергетике». Оптовый рынок электроэнергии и мощности представляет собой финансовый инструмент купли и продажи электроэнергии в России. Для покупателей участие в этом рынке дает возможность перестать платить сбытовую надбавку гарантирующему поставщику, за счет этого снижаются затраты на электроэнергию. Экономия происходит на каждом кВт·ч потребленной электроэнергии вне зависимости от объемов. Выгода ОРЭМ для продавца состоит в том, что на оптовом рынке электроэнергии спрос со стороны покупателей неэластичен. Изменение цены слабо влияет на объем потребления, предприятия не могут мгновенно сократить потребление из-за необходимости в непрекращающемся потоке энергии для поддержания работы.
Стоимость кВт·ч перебора/недобора от поданной величины рассчитывается по тарифу балансирующего рынка. В последнее время идет рост числа энергоемких потребителей, таких как центры обработки данных, предприятия с круглосуточными циклами работы и крупные городские агломерации. При этом в Российской Федерации, с одной стороны, цены на балансирующем рынке, как правило, отличаются от цен в рынке «на сутки вперед» на 10–30 % в сторону увеличения, из-за чего возрастает важность краткосрочного/среднесрочного прогнозирования необходимой электроэнергии на «рынке на сутки вперед» и формирования плана для энергосбытового предприятия [1]. С другой стороны, объем рынка данных в мире растет в среднем на 20 % в год, рынок центров обработки данных в зависимости от региона – на 10–20 %, иногда на 30 % в год. За 2018–2022 гг. рынок центров обработки данных в России вырос более чем в 2,5 раза, до 87,4 млрд руб. [2]. Недостаточная мощность, перебои с поставками электроэнергии [3], отсутствие питания в жилых кварталах и предприятиях могут существенно ухудшить инвестиционный климат региона, отпугнув потенциальных крупных потребителей и налогоплательщиков [4]. Поэтому актуальной становится задача не только прогнозирования потребления электроэнергии, но и повышения точности прогноза, которая непосредственно оказывает влияние на стабильность работы энергосистемы. Задача исследования заключается в повышении точности прогнозирования в контексте энергопотребления на основе сравнительного анализа моделей, основанных на подходах от классических статистических моделей до современных алгоритмов машинного и глубокого обучения.
Классификация подходов к прогнозированию энергопотребления и метрики оценки точности прогнозирования моделей
Данные об энергопотреблении являются временными рядами и могут быть спрогнозированы на основе тех же подходов. Необходимо учитывать, что энергопотребление характеризуется сложными и нелинейными зависимостями, выраженной сезонностью, нестационарностью и внешними факторами (метеоусловия, экономика, пандемии). Для решения задачи прогнозирования временных рядов выделяют 3 глобальных подхода: статистические модели, машинное обучение, глубокое обучение (рис. 1).
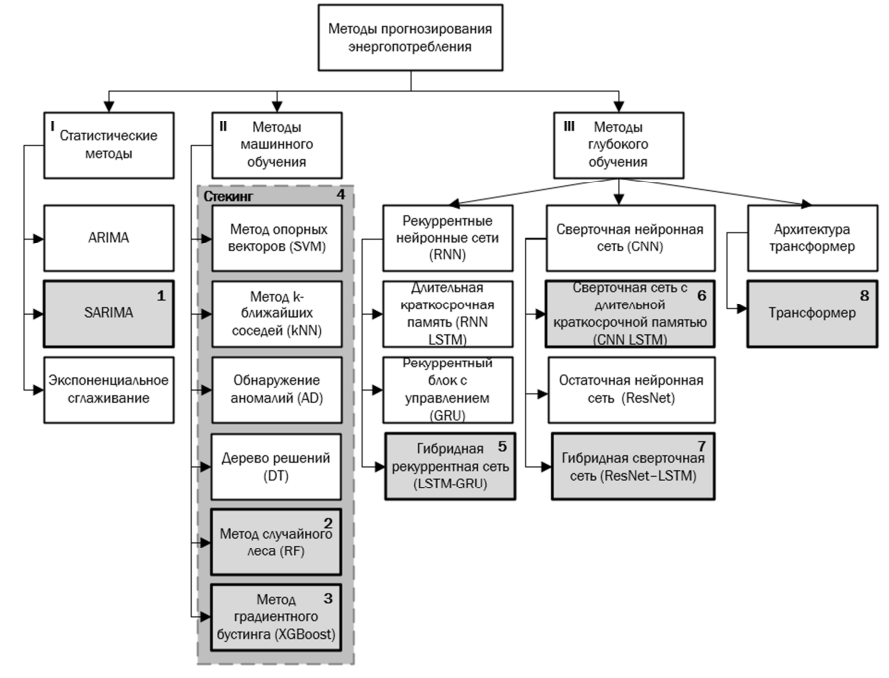
Рис. 1. Классификация методов прогнозирования энергопотребления
Fig. 1. Classification of energy consumption forecasting methods
Традиционные статистические методы прогнозирования (ARIMA, SARIMA, экспоненциальное сглаживание, см. рис. 1, I) плохо справляются с нелинейными зависимостями, сезонностью и влиянием внешних факторов (погодных, экономических и социальных) [5]. Среди статистических моделей SARIMA (см. рис. 1, 1) показывает лучшие результаты в контексте прогнозирования энергопотребления из-за учета следующих факторов: учет сезонности, комбинация стационарности и адаптивности [6]. SARIMA явно моделирует сезонные паттерны (например, суточные пики нагрузки или годовые циклы) через параметры P, D, Q, s, где P – порядок сезонной авторегрессии, D – степень сезонного дифференцирования, Q – порядок сезонного скользящего среднего, s – период сезонности (например, 12 для месячных данных). Это отличает ее от ARIMA, которая игнорирует сезонность. В исследовании [7] прогнозирования выработки ветряных электростанций SARIMA превзошла ARIMA и другие методы именно за счет оптимизации сезонных параметров.
К методам машинного обучения (см. рис. 1, II), которые чаще всего применяются для решения задачи прогнозирования временных рядов, относятся метод случайного леса Random Forest (RF), метод градиентного бустинга (XGBoost), дерево решений Decision Tree (DT), обнаружение аномалий Anomaly Detection (AD), метод k-ближайших соседей k-Nearest Neighbors (k-NN), метод опорных векторов Support Vector Machines (SVM), комбинированные модели (стекинг) [8]. В [9] было выявлено, что среди перечисленных моделей наилучшие результаты при краткосрочном прогнозировании показали модели RF (см. рис. 1, 2) и XGBoost (см. рис. 1, 3), поэтому в данной работе было решено отдельно разработать и протестировать эти модели, а остальные объединить в стекинг (см. рис. 1, 4) с добавлением XGBoost.
Методы глубокого обучения (см. рис. 1, III) разделяются на следующие категории: реккурентные нейронные сети (Recurrent neural network, RNN), сверточные нейронные сети (Convolutional neural network, CNN) и трансформеры (Transformer). Рекуррентные нейронные сети включают в себя сети с длительной краткосрочной памятью (Long Short-Term Memory, LSTM), рекуррентный блок с управлением (Gated Recurrent Unit, GRU) – две разновидности рекуррентной нейронной сети (RNN), разработанные специально для борьбы с проблемами затухания и взрыва градиента. Сеть LSTM предназначена для обучения и запоминания паттернов на длинных последовательностях данных. В отличие от стандартных RNN, которые не справляются с долгосрочными зависимостями из-за проблемы исчезающего градиента, LSTM используют уникальный механизм блокировки для регулирования потока информации. Ключом к возможностям LSTM является ее внутренняя структура, которая включает в себя «состояние ячейки» и несколько «ворот». Состояние ячейки действует как конвейерная лента, переносящая соответствующую информацию через последовательность. Ворота – вход, «забывание» и выход – представляют собой нейронные сети, которые управляют тем, какая информация добавляется, удаляется или считывается из состояния ячейки. Ворота «забывания» решают, какая информация из предыдущего состояния ячейки должна быть отброшена. Входные ворота определяют, какая новая информация из текущего входа должна быть сохранена в состоянии ячейки. Выходные ворота управляют тем, какая информация из состояния ячейки используется для генерации выходного сигнала для текущего временного шага. Такая структура ячеек LSTM позволяет модели запоминать важную информацию на протяжении многих шагов во времени, что помогает лучше понимать последовательные данные, например текст или временные ряды.
Сеть GRU, в сущности, представляет собой упрощенную LSTM. GRU объединяет ворота «забывания» и входные ворота в одни ворота «обновления» и объединяет состояние ячейки и скрытое состояние. Это делает сети GRU эффективнее с вычислительной точки зрения и быстрее в обучении, хотя в некоторых задачах они могут уступать LSTM. В [10] рассматривается гибридная модель LSTM-GRU, которая использует преимущества обеих архитектур, объединяя их возможности. Однако возможно дальнейшее совершенствование архитектуры LSTM-GRU именно для повышения точности прогноза (см. рис. 1, 5).
Сверточная нейронная сеть эффективна для обработки данных с топологией, похожей на сетку. CNN автоматически и адаптивно учится выделять иерархии признаков из входных данных. В отличие от обычных нейросетей, где каждый нейрон соединен со всеми нейронами следующего слоя, в CNN используется операция свертки. Благодаря этому сеть распознает характерные элементы в локальных участках, сохраняя пространственные связи между пикселями.
Сверточная сеть с длительной краткосрочной памятью CNN-LSTM (см. рис. 1, 6) объединяет два разных способа обработки данных. Сверточные слои сначала выделяют локальные изменения в ряду. Это резкие всплески, небольшие колебания, повторяющиеся формы, которые встречаются в почасовых данных. После этого LSTM улавливает саму логику последовательности. Она учитывает, что потребление часто зависит от предыдущих часов, от времени суток и от накопленных изменений. В результате модель не просто реагирует на отдельные пики, а понимает, как они связаны друг с другом.
Остаточная нейронная сеть (ResNet) – это тип сверточной нейронной сети, которая решает проблему затухающих градиентов благодаря «остаточным блокам» с пропускаемыми соединениями. Структура ResNet подобна ансамблю, где входной сигнал обрабатывается по множеству альтернативных путей, число которых растет с глубиной сети, что делает ResNet эффективной для построения очень глубоких моделей [11].
Гибридная сверточная сеть (ResNet-LSTM) (см. рис. 1, 7) объединяет два уровня обработки данных. Остаточные сверточные блоки выделяют локальные формы внутри ряда, такие как короткие пики, провалы и небольшие циклы, не теряя исходный сигнал благодаря пропускам связи. LSTM дополняет это, улавливая более протяженные зависимости, связанные с суточной ритмикой и плавными изменениями нагрузки. В итоге модель позволяет получить детальное и последовательное представление о данных, что делает ее наиболее подходящим выбором для задач, где важны мелкие колебания и более длинная временная структура.
Архитектура трансформер (transformer) – это нейросетевая модель, призванная эффективнее решать задачи many-to-many (seq2seq) по преобразованию одной последовательности в другую. Стандартная модель трансформера (см. рис. 1, 8) состоит из двух блоков: кодировщика (encoder) и декодировщика (decoder) [12]. На вход кодировщику поступает входная последовательность из T токенов (слов), каждый из которых кодируется D-мерным эмбеддингом, обучаемым вместе с настройкой самой сети. Но информация о расположениях токенов внутри последовательности теряется. Чтобы модели в явном виде сообщить, какие токены где располагались, к эмбеддингу каждого токена на входе в декодировщик прибавляется эмбеддинг той же размерности, кодирующий абсолютное расположение эмбеддинга. Это называется позиционным кодированием. Выходом кодировщика является T эмбеддингов входных элементов последовательности, уточненных с учетом контекста всей последовательности.
Проведенный анализ моделей позволил выделить для исследования, совершенствования, адаптации и оценки точности 8 методов прогнозирования (см. рис. 1, 1–8). Оценку точности прогноза энергопотребления на основе выбранных методов будем осуществлять с помощью следующих метрик:
– среднеквадратичная ошибка (Mean Squared Error, MSE) – это среднее значение квадратов разностей между наблюдаемыми значениями на практике и значениями, предсказанными моделью
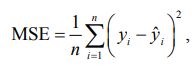
где n – число примеров в обучающей выборке; yᵢ – фактическое значение; ŷᵢ – прогноз;
– среднеквадратическое отклонение (Root Mean Squared Error, RMSE) показывает, насколько в среднем отличаются предсказанные моделью значения от реальных. RMSE напрямую отражает величину ошибки предсказания в тех же единицах, что и исследуемый показатель. RMSE полезен, когда нужно уменьшить ошибки и оценить точность прогнозирования модели в понятных величинах:
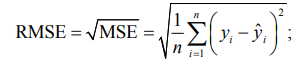
– средняя абсолютная ошибка прогноза (Mean Absolute Error, MAE) используется для измерения средней величины ошибок между предсказанными и фактическими значениями. В отличие от метрик, которые возводят ошибки в квадрат (например, MSE), MAE одинаково учитывает все ошибки, что делает ее интуитивно понятной и устойчивой к выбросам:
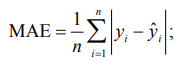
– средняя абсолютная процентная ошибка (Mean Absolute Percentage Error, MAPE) является процентным аналогом средней абсолютной ошибки (MAE) и показывает, на сколько процентов в среднем предсказания модели отличаются от реальных значений:
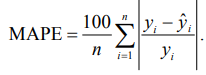
Например, MAE = 87,5 МВт показывает, что в среднем модель ошибается на 87,5 МВт. MAPE = = 1,92 % означает, что в среднем модель ошибается на 1,92 %. В работе [13] установлено, что показатель MAPE в пределах 2–4 % является допустимым как для торговли на рынке ОРЭМ, так и для прогнозирования энергопотребления в расчете устойчивости энергосистемы и планирования строительства новых энергообъектов. В качестве набора данных использовался датасет Open Power System Data с почасовыми показателями энергопотребления [14]. При разработке, тестировании, анализе моделей, а также визуализации использовались язык программирования Python, библиотеки и фреймворки Sklearn, Statsmodels, Pandas, Plotly, Numpy, Itertools, Tensorflow, Xgboost, Torch, Math.
Адаптация и оценка точности прогнозирования методов прогнозирования энергопотребления
Рассмотрим детально выделенные методы прогнозирования для анализа временных рядов на основе данных датасета по энергопотреблению. Для этого сведем в таблицу результаты тестирования моделей прогнозирования (см. рис. 1, 1–8) в соответствии с описанными ранее характеристиками точности прогнозирования моделей.
Итоговые результаты работы моделей
The final results of the models' work
|
Позиция в списке моделей |
Модель |
MSE, |
MAE, |
RMSE, МВт |
MAPE, % |
|
1 |
Гибридная рекуррентная сеть LSTM-GRU (см. рис. 1, 5) |
1 565 464,76 |
967,09 |
1 251,19 |
1,86 |
|
2 |
Transformer (улучш.) (см. рис. 1, 8) |
2 038 927,88 |
1 118,52 |
1 427,91 |
2,25 |
|
3 |
Гибридная сверточная сеть (ResNet-LSTM) (см. рис. 1, 7) |
2 147 756,50 |
1 161,02 |
1 465,52 |
2,30 |
|
4 |
Метод случайного леса (RF) (см. рис. 1, 2) |
3 249 246,09 |
1 302,85 |
1 802,57 |
2,62 |
|
5 |
Метод градиентного бустинга (XGBoost) (см. рис. 1, 3) |
3 211 426,49 |
1 327,25 |
1 792,05 |
2,66 |
|
6 |
Стекинг (см. рис. 1, 4) |
3 480 176,03 |
1 349,36 |
1 865,52 |
2,71 |
|
7 |
Transformer (см. рис. 1, 8) |
3 492 326,75 |
1 427,93 |
1 868,78 |
2,80 |
|
8 |
Сверточная сеть с длительной краткосрочной памятью (CNN LSTM) (см. рис. 1, 6) |
4 882 154,95 |
1 734,98 |
2 209,56 |
3,39 |
|
9 |
SARIMA (см. рис. 1, 1) |
58 538 385,61 |
6 022,35 |
7 651,04 |
12,12 |
SARIMA = AR (авторегрессия, учитывает инерцию временного ряда) + MA (скользящее среднее, учитывает случайные выбросы) + I (интегрирование, работа с трендом) + S (сезонность, учет паттернов). Интегрированная компонента (I) делает ряд стационарным через дифференцирование (d (порядок несезонного дифференцирования) и D (порядок сезонного дифференцирования)), что критично для данных с трендами (например, рост потребления из-за урбанизации) [15]. Авторегрессия (AR) и скользящее среднее (MA) работают с несезонными лагами и ошибками, а их сезонные аналоги (SAR, SMA) – с сезонными лагами. Это позволяет моделировать краткосрочные шумы и долгосрочные циклы одновременно [16]. Результаты тестов модели SARIMA на исследуемом датасете приведены в таблице и на рис. 2.
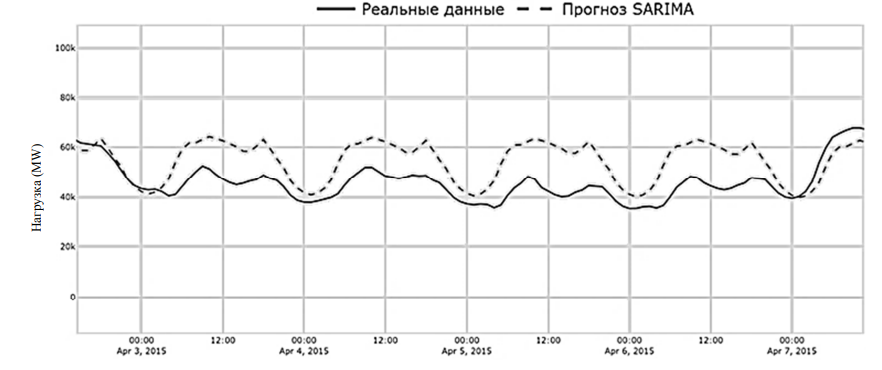
Рис. 2. Фрагмент результатов прогноза модели SARIMA
Fig. 2. A fragment of the SARIMA model forecast results
Метод случайного леса. RF представляет собой универсальный алгоритм машинного обучения, основанный на ансамбле решающих деревьев. Основная идея заключается во введении случайности при построении некоррелированных деревьев. Случайность достигается через бутстрап, когда каждое дерево обучается на случайной выборке с повторениями из обучающих данных, и через случайный выбор признаков при разбиении узлов, что предотвращает доминирование отдельных признаков. Объединяя прогнозы деревьев, модель снижает дисперсию и обеспечивает более высокую точность, чем отдельное дерево. Алгоритм включает создание случайных выборок из исходного набора данных, построение дерева для каждой выборки, получение прогнозов и агрегирование результатов голосованием. В отличие от одиночных деревьев, склонных к переобучению, RF формирует более устойчивую и обобщающую модель. RF успешно применялся для прогнозирования временных рядов, включая энергопотребление [17].
Метод градиентного бустинга. XGBoost также являются ансамблевым методом, основанным на деревьях решений. Однако он использует другую стратегию, называемую бустинг. XGBoost строит систему предсказательного моделирования путем последовательного добавления простых моделей, обычно деревьев решений, для исправления ошибок, допущенных предыдущими моделями. Каждое новое дерево обучается предсказывать остаточные ошибки предыдущих, эффективно учась на ошибках для повышения общей точности. Отличительной особенностью XGBoost являются производительность и оптимизация. Ключевые особенности включают: выполнение построения деревьев параллельно, что значительно ускоряет процесс обучения модели; регуляризацию L1 и L2 для предотвращения перебора, делая модели более обобщенными; обработку недостающих данных (в XGBoost встроена возможность обработки отсутствующих значений в наборе данных, что упрощает предварительную обработку данных); оптимизацию кэша для оптимального использования аппаратных ресурсов, что еще больше увеличивает скорость вычислений. Результаты тестов моделей RF и XGBoost на исследуемом датасете приведены в таблице. Фрагмент графика прогноза показан на рис. 3.
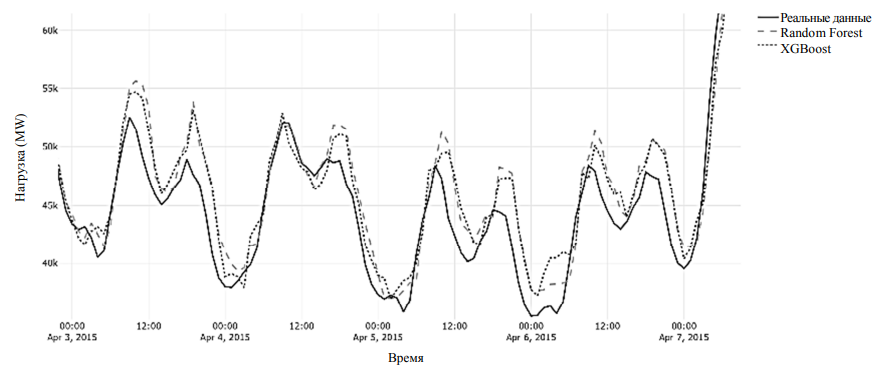
Рис. 3. Фрагмент прогноза RF и XGBoost
Fig. 3. A fragment of the RF and XGBoost forecast
Стекинг представляет собой метод ансамблирования, в котором несколько моделей объединяются через мета-модель. Базовые модели обучаются на исходных данных и делают прогнозы, которые превращаются в новые признаки, называемые мета-признаками. Мета-модель обучается на этих признаках и исходных значениях, чтобы найти оптимальную комбинацию прогнозов и сформировать итоговый результат. Пример: три базовые модели LR, DT и k-NN формируют мета-признаки, финальной моделью может быть Ridge-регрессия, которая обучает веса для каждой модели по формуле
где P – итоговый прогноз; PLR – прогноз LR; PDT – прогноз DT; Pk-NN – прогноз k-NN.
«Чистые прогнозы» создаются на данных, не использованных при обучении базовых моделей, чтобы избежать переобучения мета-модели. В разработанной модели два уровня. Первый уровень включает экспертов: DT, RF и XGBoost анализируют сложные нелинейные взаимосвязи, k-NN ищет исторические аналоги, AD оценивает аномалии, LSTM учитывает временной контекст и долгосрочные зависимости. Второй уровень – это мета-модель, которая получает прогнозы всех экспертов и учится распределять доверие в зависимости от ситуации. Итоговый прогноз формируется как взвешенная комбинация прогнозов базовых моделей, обеспечивая более высокую точность. Схема модели показана на рис. 4.
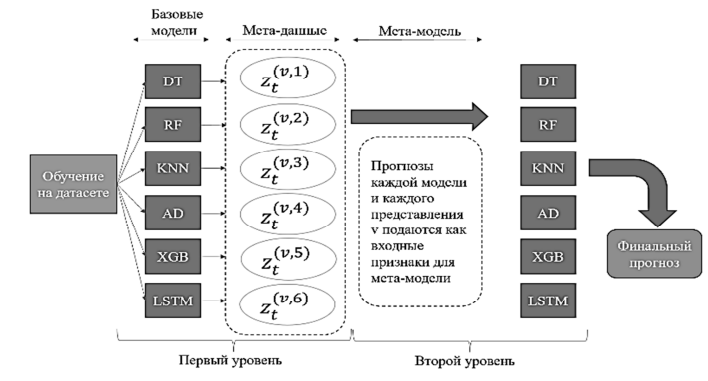
Рис. 4. Стекинг. Гибридная модель: z(t)(v, n) – мета-признаки
Fig. 4. Stacking. Hybrid model: z(t)(v, n) – meta-features
LSTM в контексте стекинга работает как эксперт по долгосрочным и сложным временным трендам. Модель добавляет в ансамбль информацию, которую другие модели либо не могут извлечь, либо извлекают хуже. Отдельно данная модель рассмотрена ранее. Результаты тестов усовершенствованной модели стекинга на исследуемом датасете приведены в таблице.
В модели LSTM-GRU LSTM отвечает за улавливание долгосрочных зависимостей, запоминая ключевую информацию на протяжении всей последовательности, а GRU фокусируется на недавних наблюдениях и наиболее значимых признаках, сжимая информацию. В результате модель одновременно учитывает как глобальные тенденции (долгосрочные паттерны), так и локальные колебания, что важно для энергопотребления, где наблюдаются как устойчивые суточные и недельные циклы, так и краткосрочные всплески. Результаты тестов модели LSTM-GRU стекинга приведены в таблице и на рис. 5.
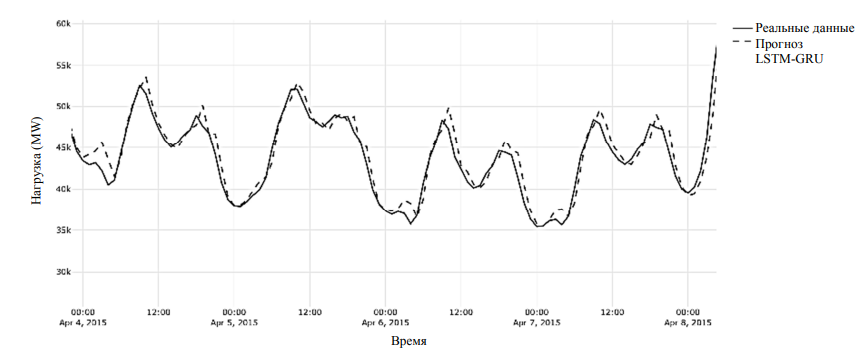
Рис. 5. Фрагмент прогноза LSTM-GRU
Fig. 5. Fragment of the LSTM-GRU forecast
Такая высокая точность обусловлена во многом тем, что LSTM улавливает долгосрочные зависимости: помнит важную информацию из начала 24-часового окна; распознает суточные паттерны (ночные спады, утренние подъемы). В свою очередь, GRU эффективно сжимает информацию: извлекает наиболее важные признаки из всей последовательности; фокусируется на последних наблюдениях, которые важны для прогноза. Это можно объяснить, если вручную проанализировать часть датасета, как показано на рис. 6.

Рис. 6. Пример ручного анализа части набора данных
Fig. 6. An example of manual analysis of a part of a dataset
Как видно, в 24-часовом окне присутствуют суточные паттерны.
Гибридная модель LSTM-CNN представляет собой сложную структуру, состоящую из нескольких слоев. Модель состоит из последовательного стека слоев. На первом этапе используется одномерная сверточная сеть с 32 фильтрами и ядром размера 3, что позволяет автоматически извлекать локальные временные закономерности. Далее применяется слой, сокращающий временную размерность и выделяющий наиболее информативные признаки. Полученная последовательность поступает в рекуррентный слой LSTM с 50 скрытыми состояниями, который моделирует долгосрочные зависимости временного ряда. Для предотвращения переобучения используется механизм случайного отключения части внутренних элементов (0,2). На финальном этапе предсказание формируется с помощью линейного преобразователя, агрегирующего полученные признаки в одно выходное значение. Обучение проводится методом оптимизации Adam с функцией потерь MSE. На рис. 7 показан фрагмент прогноза LSTM-CNN.
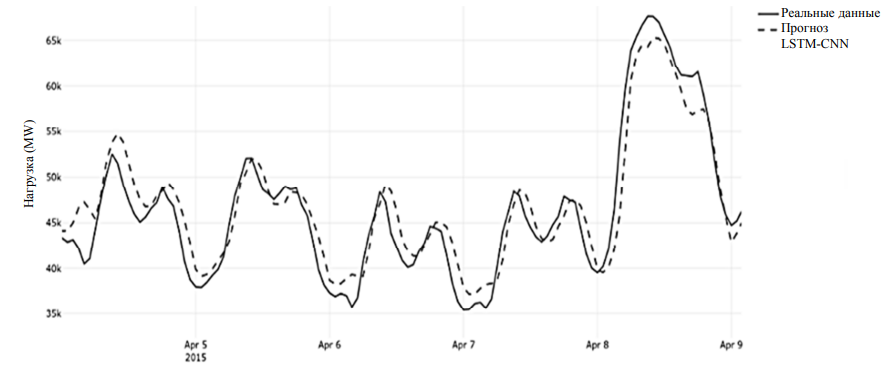
Рис. 7. Фрагмент графика прогнозирования модели LSTM-CNN
Fig. 7. A fragment of the prediction graph of the LSTM-CNN model
Была разработана гибридная модель ResNet-LSTM, которая объединяет сверточные блоки с остаточными связями и слой LSTM. На вход подаются последовательности из 24 предыдущих значений, которые сначала проходят через два ResNet-подобных блока Conv1d с активацией ReLU и пропусками. Conv1d – это одномерная свертка вдоль временной оси, которая позволяет извлекать локальные структуры во временном ряде, а пропуски сохраняют исходную информацию и стабилизируют обучение. Необходимость наличия двух ResNet блоков обусловлена тем, что в исследованиях [18] было показано, что один блок может пропустить сложные зависимости, три блока и больше ведут к переобучению на небольших данных. Таким образом, два блока – это оптимальный баланс для временных рядов, где первый блок выделяет простые паттерны (пики, провалы), а второй блок выделяет сложные паттерны (комбинации простых паттернов). После сверточной обработки данные переставляются в формат последовательности и подаются в LSTM, который учитывает долгосрочные зависимости временного ряда. Последний скрытый выход LSTM преобразуется полносвязным слоем в одно значение, воспринимаемое как прогноз. Для нормализации данных используется метод MinMaxScaler, который масштабирует значения в диапазон от 0 до 1, что помогает ускорить обучение и стабилизировать градиенты. Такая комбинация сверток и рекуррентного слоя позволяет модели одновременно учитывать краткосрочные колебания и долгосрочные тенденции в потреблении электроэнергии. График прогнозирования частично показан на рис. 8.
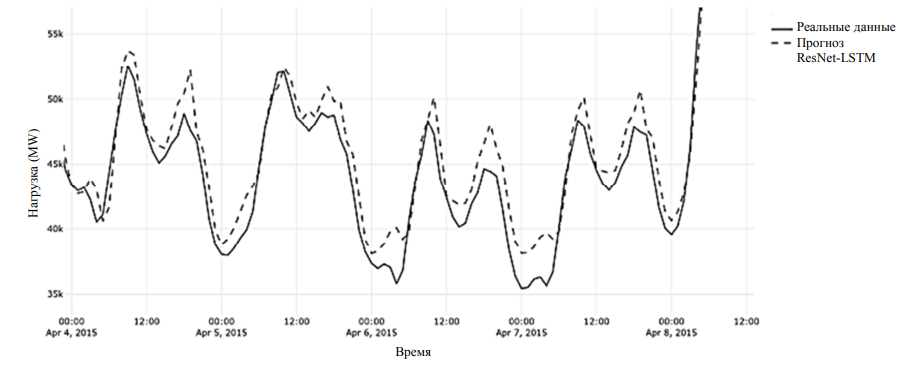
Рис. 8. Фрагмент графика прогнозирования модели ResNet-LSTM
Fig. 8. A fragment of the ResNet-LSTM model prediction graph
В модели Transformer на вход декодировщику подается выходная последовательность, сдвинутая на один токен начала последовательности и завершенная токеном конца последовательности с дополнением токеном заполнения для выравнивания по максимальной длине в минибатче. Последовательности обрабатываются минибатчами. Максимальная длина минибатча T определяется как
Более короткие последовательности после токена конца последовательности дополняются токеном заполнения, чтобы все имели одинаковую длину для параллельной обработки. Кодировщик выдает эмбеддинг для каждого токена, к которому применяется линейный слой и функция активации SoftMax, формируя вероятностное распределение слов и позволяя предсказать следующее слово. Результаты тестирования модели Transformer приведены в таблице и на рис. 9.
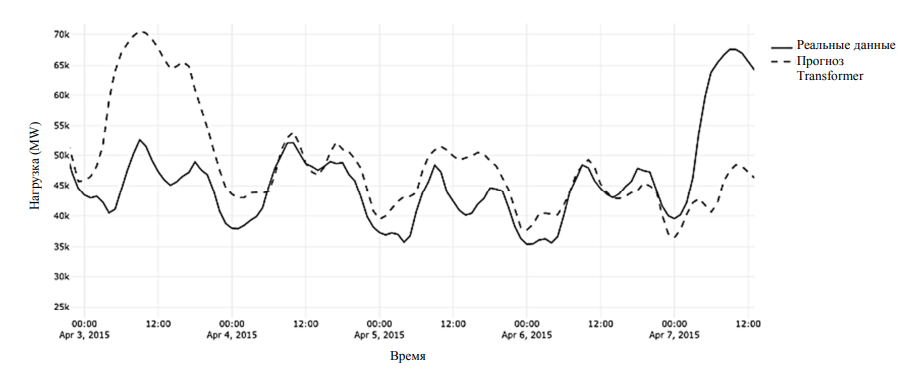
Рис. 9. Фрагмент графика прогноза модели Transformer
Fig. 9. Fragment of the forecast graph of the Transformer model
Несмотря на то, что MAPE, равный 2,80 %, на текущий момент не является лучшим результатом среди всех протестированных моделей, было решено попытаться усовершенствовать данную модель трансформера [19, 20].
Улучшенная модель Transformer была реализована в соответствии с рекомендациями из других похожих исследований [19, 20], а также на основе выводов, сделанных благодаря таким средствам интерпретации работы нейросетей и аналитики, как SHAP.
Размерность модели увеличена с 32 до 64, что позволяет скрытым состояниям лучше кодировать сложные паттерны. Количество слоев трансформера увеличено с 2 до 3, теперь модель может извлекать более сложные иерархические зависимости. Размер скрытого слоя FFN (Feed Forward Network) расширен с 64 до 256, это повысило способность к нелинейным преобразованиям. Добавлены методы регуляризации и оптимизации, а также Layer Normalization, которая контролирует масштаб активаций и снижает внутренний сдвиг распределений. Для стабилизации обучения используется ограничение величины градиентов (gradient clipping), что предотвращает их резкий рост. Инициализация весов выполнена методом Xavier, обеспечивающим правильный масштаб начальных значений и ускоряющим сходимость. Функция активации ReLU заменена на GELU, которая обеспечивает плавную нелинейность и более точную передачу градиентов, приближаясь к поведению dropout, техники, которая случайным образом «отключает» часть нейронов во время обучения, чтобы модель не переобучалась. Как видно из метрик, внесенные изменения положительно повлияли на точность прогноза. На рис. 10 показана часть графика прогнозирования обновленной модели.
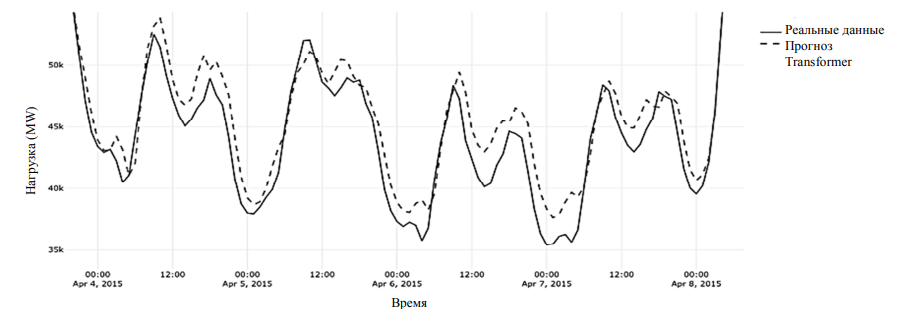
Рис. 10. Фрагмент графика прогноза улучшенной модели Transformer
Fig. 10. A fragment of the forecast graph of the improved Transformer model
Совокупное сравнение метрик всех исследованных моделей, отсортированное от лучших показателей к худшим, приведена в таблице. Модель LSTM-GRU показала наилучшие результаты, это можно объяснить тем, что она объединяет два рекуррентных механизма – LSTM (запоминает долгосрочные зависимости) и GRU (работает быстрее и устойчивее), тогда как датасет имеет ярко выраженную суточную и недельную цикличность, а также плавные переходы – именно то, где рекуррентные сети сильны, из-за чего сеть оптимально улавливает структуру временного ряда и не переобучается. В качестве улучшения можно протестировать разное число предыдущих временных шагов, которые подаются на вход модели для предсказания следующего значения, например 12, 24, 48, 72 временных шага (т. е. полсуток, сутки, двое суток, трое суток), добавить автоматическую остановку, если точность на валидационной выборке перестает улучшаться.
Заключение
Были рассмотрены проблемы актуальности прогнозирования энергопотребления в контексте торговли на оптовом рынке и проектировании энергоснабжения. На основе проведенного глубокого анализа моделей и методов прогнозирования энергопотребления была определена эффективность тех или иных моделей и методов, даны объяснения полученных результатов, описаны преимущества и выявлены недостатки исследованных подходов, даны рекомендации по улучшению результатов. Проведенное исследование не только позволило определить наиболее эффективные подходы для краткосрочного прогнозирования энергопотребления, но и выявило направления, в которых эти модели могут развиваться дальше. Эксперименты показали, что даже хорошо зарекомендовавшие себя архитектуры, такие как Transformer и ResNet, чувствительны к подбору гиперпараметров и качеству предварительной обработки данных. Это означает, что дальнейшее повышение точности возможно не только за счет усложнения моделей, но и благодаря более тонкой настройке их структуры, корректному выбору размера входного окна, применению регуляризации и оптимизации. Кроме того, комбинирование моделей различных типов, как продемонстрировали гибридные подходы, может дать дополнительный прирост точности, что делает дальнейшее развитие гибридных подходов перспективным направлением. В задаче прогнозирования энергопотребления важно корректное сочетание методов и адаптация моделей под структуру данных для достижения высокой точности.
1. Cvedeniya o sostavlyayushchih v konechnom tarife dlya potrebitelya i mekhanizme tarifoobrazovaniya: prilozhenie [Information about the components in the final tariff for the consumer and the tariff setting mechanism: appendix]. Rosseti Yug. Available at: https://rosseti-yug.ru/upload/iblock/5cd/m_i_s_tarif.pdf (accessed: 30.09.2025).
2. Povyshennye nagruzki. Kak razvitie COD vliyaet na energopotreblenie v Rossii [Increased workload. How does data center development affect energy consumption in Russia]. Sber PRO. 2024. 21 avgusta. Available at: https://sber.pro/publication/povishennie-nagruzki-kak-razvitie-tsod-vliyaet-na-energopotreblenie-v-rossii/ (accessed: 30.09.2025).
3. Minenergo planiruet predlozhit' novye podhody k prognozirovaniyu potrebleniya energii [The Ministry of Energy plans to propose new approaches to forecasting energy consumption]. Neftegaz.RU. 17 iyulya 2024. Available at: https://neftegaz.ru/news/energy/844339–minenergo–planiruet–predlozhit–novye–podkhody–k–prognozirovaniyu–potrebleniya–energii/ (accessed: 11.09.2025).
4. Opadchij F. Dal'nejshij nekontroliruemyj rost svyazannoj s majningom nagruzki v otdel'nyh chastyah EES ne-vozmozhno obespechit' tradicionnymi sposobami razvitiya energosistemy [Further uncontrolled growth of the mining-related load in certain parts of the UES cannot be ensured by traditional ways of developing the energy system]. AO «Sistemnyj operator EES». Press-reliz. 2024. 26 aprelya. Available at: https://www.so-ups.ru/news/press-release/press-release-view/news/24642/ (accessed: 11.09.2025).
5. Turkova K. A., Molyavina Yu. O. Ocenka modelej analiza i prognozirovaniya stohasticheskih vremennyh ryadov [Evaluation of stochastic time series analysis and forecasting models]. Cifrovoe obshchestvo: nauchnye iniciativy i novye vyzovy: sbornik nauchnyh trudov po materialam VI Vserossijskoj nauchno-prakticheskoj konferencii. Moscow, 2024. Pp. 285-292.
6. Mahanta N., Talukdar R. Forecasting of Electricity Consumption by Seasonal Autoregressive Integrated Moving Average Model in Assam, India. International Journal of Energy Economics and Policy, 2024, no. 5, pp. 393-400.
7. Szostek K., Mazur D., Drałus G., Kusznier J. Analysis of the Effectiveness of ARIMA, SARIMA, and SVR Models in Time Series Forecasting: A Case Study of Wind Farm Energy Production. Energies, 2024, no. 17, pp. 35-53.
8. Bin Syed A., Hasan R., Chowdhury N., Rahman H., Ahmed I. A systematic review of time series algorithms and analytics in predictive maintenance. Decision Analytics Journal, 2025, no. 15, pp. 187-203.
9. Mystakidis A., Ntozi E., Afentoulis K., Koukaras P., Gkaidatzis P., Ioannidis D., Tjortjis C., Tzovaras D. Energy generation forecasting: elevating performance with machine and deep learning. Springer, 2023, no. 105, pp. 1623-1645.
10. Sari Y., Arifin Y., Novitasari N., Faisal M. Deep Learning Approach Using the GRU-LSTM Hybrid Model for Air Temperature Prediction on Daily Basis. International Journal of Intelligent Systems and Applications in Engineering, 2022, no. 3, pp. 430-436.
11. Kondaiah V., Saravanan B. A modified deep residual network for short-term load forecasting. Frontiers in Energy Research, 2022, no. 10, pp. 44-56.
12. Vaswani A., Shazeer N., Parmar N., Uszkoreit J., Jones L., Gomez A., Kaiser L., Polosukhin I. Attention Is All You Need. Proceedings of the 31st International Conference on Neural Information Processing Systems. New York, Curran Associates Inc., 2017. Pp. 6000-6010.
13. Perry B. How to Evaluate Power Demand Forecasts. Available at: https://blog.yesenergy.com/yeblog/how-to-evaluate-power-demand-forecasts (accessed: 11.09.2025).
14. Time series. Data Platform. Available at: https://data.open–power–system–data.org/time_series/ (accessed: 11.09.2025).
15. Zhang X., Cao W. Research on Time Series Fore-casting Method Based on Autoregressive Integrated Moving Average Model with Zonotopic Kalman Filter. Sustainability, 2025, no. 17, pp. 21-39.
16. Khalil A., Ullah S., Ahmad Khan S., Manzoor S., Gul A., Shafiq M. Applying Time Series and a Non-Parametric Approach to Predict Pattern, Variability, and Number of Rainy Days Per Month. Polish Journal of Envi-ronmental Studies, 2017, no. 2, pp. 635-642.
17. Dudek G. A Comprehensive Study of Random Forest for Short-Term Load Forecasting. Energies, 2022, no. 20, pp. 80-99.
18. Zeiler M., Fergus R. Visualizing and Understanding Convolutional Networks. Computer Vision - ECCV 2014, 2014, no. 8, pp. 818-833.
19. Pires T., Lopes A., Assogba Y., Setiawan H. One Wide Feedforward is All You Need. arXiv, 2023, no. 1, pp. 1031-1044.
20. Press O., Smith N., Levy O. Improving Transformer Models by Reordering their Sublayers. Association for Computational Linguistics, 2020, no. 58, pp. 2996-3005.