Russian Federation
Russian Federation
Replacing metal electrical conductors with fiber-optic elements in the marine and river fleets leads not only to metal savings, but also to increased energy efficiency and fire safety, since quartz fiber transmits higher optical power than copper wire ‒ similar electrical power. A promising direction in the management of automatic electric drives and coastal electrical installations of water transport is the use of a laser with a Q modulator. For example, by controlling a laser using a Q modulator on a standing unmodulated ultrasonic wave, chaotic “peak” generation is suppressed and the self-oscillating mode used in practice is obtained. The use of such a laser in an automatic electric drive gives intelligent properties to the control of a water transport facility. However, the causes of self-oscillations and the methods of controlling the auto-oscillations of dynamic objects have not yet been sufficiently studied. In this paper, using a digital model (DM) created on the basis of a three-level system of laser velocity differential equations, the phase and time characteristics of laser self-oscillations as a dynamic system for con-trolling energy losses for fixed values of the energy delivery rate are obtained. The digital model makes it possible to study in detail the self-oscillatory process from the moment of the origin of a closed trajectory, the appearance and elimination of the second harmonic to periodic undamped oscillations in the form of limit cycles in a wide range of control coefficient changes proportional to energy losses. The use of DM makes it possible to register dynamic processes on the phase plane and time sweep in a wide range of changes in delivery rates and energy losses. The calculation results are applicable to the optimization of automated electric drives and coastal electric installations of water transport with laser devices. The proposed DM allows conducting similar studies of dynamic systems of different nature, having a structure of energy levels.
figure model, control, auto oscillatory of laser as dynamical system, automation, optimization, electric drive, laser device, coastal electrical installation, water transport
Введение
Оптоэлектронные устройства на базе лазеров внедряются в комплексы связи, управления объектов морского и речного флота [1, 2]. Структурная схема автоматического электропривода объекта водного транспорта с лазерным устройством предполагает, что лазер может входить в состав оптоэлектронного регулятора и выполнять для исполнительного устройства функции усилителя сигналов с выхода измерительно-информационного комплекса [3].
Динамика многоуровневой системы определяется соотношением вероятностей переходов атомов (заряженных частиц) между уровнями с учетом разрешенных и запрещенных переходов. Долгоживущие (метастабильные) уровни позволяют накапливать активные носители заряда, переходящие в дальнейшем на нижележащие энергетические уровни с излучением квантов энергии (фотонов). Примером служат трех- и четырехуровневые лазеры, в которых для усиления потока фотонов применены оптические резонаторы, позволяющие фотонам многократно проходить сквозь активную среду (АС) лазера. С увеличением объема АС возрастает число генерируемых типов колебаний (мод) и появляется хаотическое «пичковое» излучение из-за неоднородности усиления в каналах разных мод, что снижает энергоэффективность лазера. Экспериментально было показано, что многомодовый рубиновый лазер при возбуждении в модуляторе добротности (МД) перпендикулярно оси резонатора немодулированной стоячей ультразвуковой волны перестает генерировать хаотические «пички» и начинает излучать в режиме саморегулирования периодическую последовательность импульсов. Частота повторения излучаемых импульсов определяется не частотой ультразвука, а зависит от интенсивности ультразвука и мощности накачки (скорости доставки энергии). Можно полагать, что внутрирезонаторная дифракция Рамана – Ната на стоячей ультразвуковой волне связывает все области АС в пространственно-энергетический однородный континуум для лазерного излучения, что стимулирует самоорганизуемое поведение лазера [4]. Причины автоколебаний, методы управления автоколебаниями лазера как динамической системы требуют комплексного изучения. В настоящей работе предложена цифровая модель, с помощью которой осуществлено модельное управление автоколебаниями лазера как динамической системы; получены фазовые и временные характеристики в зависимости от скорости потерь для заданных значений скорости доставки энергии.
Модель управления автоколебаниями лазера как динамической системы
Адекватная модель для трехуровневого лазера может быть записана в виде системы двух дифференциальных уравнений [5, 6]:
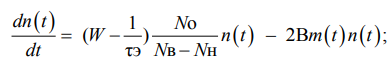(1)
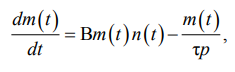(2)
где системные переменные: n(t) – приведенная населенность верхнего уровня лазерного перехода; m(t) – приведенное число фотонов; t – время; параметры: W – скорость накачки; τэ – эффективное время жизни возбужденного состояния АС; Nо = Nв + Nн – общая населенность лазерного перехода: Nв ‒ верхнего уровня, Nн – нижнего уровня; B – эйнштейновский коэффициент; Bm(t) – скорость индуцированных переходов; τр – время жизни фотона в резонаторе, τр = 2L / (Cα), где L, C, α – длина резонатора, скорость света, потери излучения соответственно.
Коэффициент 2 системы (1), (2) учитывает, что в трехуровневой модели увеличение количества фотонов на единицу сопровождается уменьшением на единицу населенности верхнего уровня лазерного перехода. Наличие в уравнениях квадратичной нелинейности свидетельствует о возможности автоколебательной динамики системы.
Введем новые обозначения согласно синтаксису MATLAB.
Системные переменные: x(t) = n(t) – пропорциональна действующей концентрации населенности, y(t) = m(t) – пропорциональна числу квантов энергии (фотонов); коэффициенты: «k» = (W ‒ 
) ×
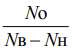– характеризует скорость доставки энергии, «c»*y(t) – характеризует скорость индуцированных переходов, «d» = 
~ α ‒ управляющий коэффициент, пропорциональный потерям энергии. Исследуемый объект имеет численные значения коэффициентов, причем «k», «c»*y(t), «d» имеют размерность 1 / с, где с – секунда.
Система дифференциальных уравнений при-
мет вид
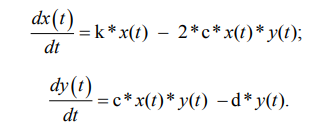
В матричной форме
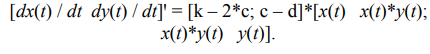
Для расчетов применен файл sah1064dst.m с встроенной строкой [Lorenz], содержащей оператор @(tx), решатель ode45 [7]. Моделирование выполняется на временном интервале t0 = 0, t1 = 10 c. Вектор начальных условий [2–5]:
% sah1064dst.m
k = 10, c = 1, d = 0;
[Lorenz]=@(t, x) [k*x(1) – 2c*x(1)*x(2); c*x(1)* – d*x(2)];
[t, x] = ode45(Lorenz, [0 10],[2,5]);
plot(x(:,1), x(:2)),grid
title (‘Аттрактор’)
xlabel (‘x(t)’);
ylabel (‘y(t)’);
%Для вывода временных характеристик:
plot(t,x(:,1),t,x(:,2)),grid
axis([0 1 6 4])
title(ꞌВременные характеристикиꞌ)
xlabel(ꞌВремя:t,cꞌ);
ylabel(ꞌПоток фотонов: y(t), относительные единицыꞌ);
Фазовые и временные характеристики
На рис. 1 представлены фазовые диаграммы
и временные характеристики трехуровневой динамической системы для фиксированных значений коэффициентов «k», «c» и разных значений коэффициента управления «d».
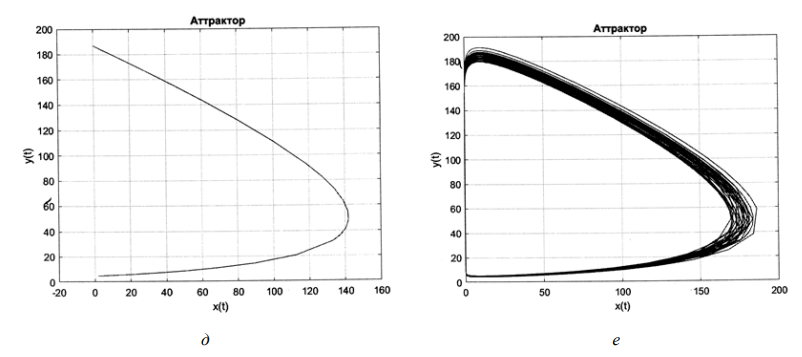
Рис. 1. Динамика системы уравнений (3), (4) при постоянных коэффициентах «k» = 100, «c» = 1
в зависимости от значений параметра управления «d»: 0 (а, в), 1 (д), 3 (б, г), 10 (е);
а, б, д, е, – аттракторы; в, г – временные характеристики
(по оси ординат отложены переменные x(t), y(t) в относительных единицах)
Fig. 1. Dynamics of the equations system (3), (4) at constant coefficients “k” = 100, “c” = 1 depending on the values
of the control parameter “d”: 0 (а, в), 1 (д), 3 (б, г), 10 (е); а, б, д, е, – attractors; в, г – time characteristics
(by ordinate axis placed variable x(t), y(t) in relative units)
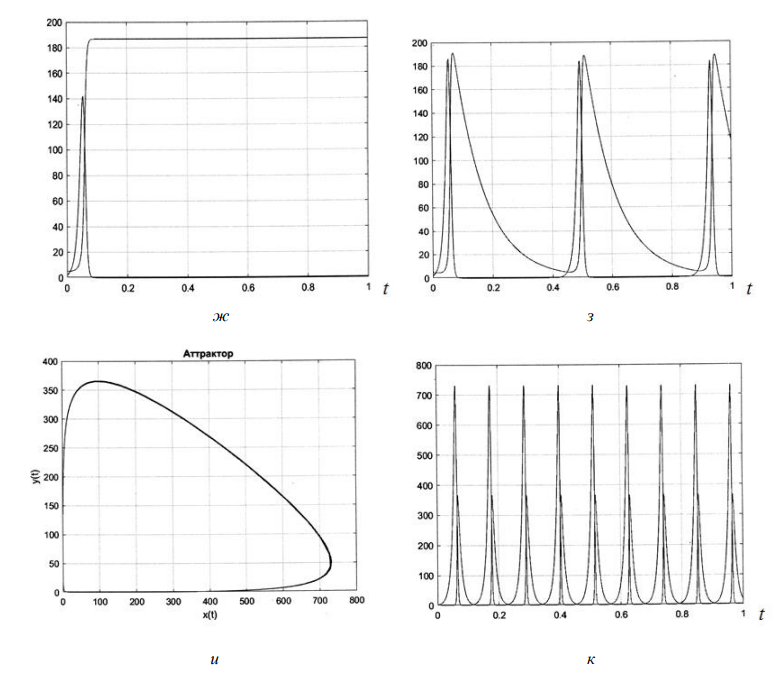
Рис. 1 (окончание). Динамика системы уравнений (3), (4) при постоянных коэффициентах «k» = 100, «c» = 1
в зависимости от значений параметра управления «d»: 1 (ж), 10 (з), 100 (и, к); и – аттракторы;
ж, з, к – временные характеристики (по оси ординат отложены переменные x(t), y(t) в относительных единицах)
Fig. 1 (ending). Dynamics of the equations system (3), (4) at constant coefficients “k” = 100, “c” = 1
depending on the values of the control parameter “d”: 1 (ж), 10 (з), 100 (и, к); и – attractors;
ж, з, к – time characteristics (by ordinate axis placed variable x(t), y(t) in relative units)
Система уравнений (3), (4) управляема в широком диапазоне значений коэффициента «d», определяющего потери квантов энергии (фотонов) (см. рис. 1). При «d» ≤ 0 автоколебательность «запрещена» (см. рис. 1, а, в). При «d» ≥ 0 система проходит несколько этапов автоколебательного движения. Так, при «d» = 1 только зарождается циклическое движение (см. рис. 1, д, ж). При «d» = 3 система демонстрирует появление второй гармоники (рис. 1, б, г). При дальнейшем развитии динамики вторая гармоника не поддерживается, наблюдается на фазовой плоскости рост ширины полосы непересекающихся витков и на временной зависимости – равенство частот повторения и амплитуд импульсов переменных x(t) и y(t), «d» = 10 (см. рис. 1, е, з). С ростом частоты автоколебаний может наблюдаться слияние витков около предельного цикла и превышение амплитуды импульсов переменной y(t) над амплитудой импульсов переменной x(t) при той же частоте их повторения, например двойное превышение при «d» = 100 (см. рис. 1, и, к). Исследованные асимптотически устойчивые стационарные движения можно рассматривать как аттракторы – притягивающие множества [8].
Отметим, что обнаруженное превышение амплитуды импульсов переменной y(t) над амплитудой импульсов переменной x(t) с ростом частоты автоколебаний наблюдается при постоянной скорости накачки, характеризуемой коэффициентом «k» = 100. Этой скорости накачки уже недостаточно для выравнивания амплитуд импульсов переменных x(t) и y(t) на частоте следования импульсов fи = 8,9 Гц (см. рис. 1, и, к). Следовательно, недостаточная скорость накачки накладывает ограничение на максимальную частоту автоколебаний. Максимальная частота автоколебаний рассматриваемой системы при «k» = 100; «c» = 1; «d» = 100 не превышает fи max = 10 Гц. Аналогичное ограничение действует при кратном уменьшении коэффициента накачки «k» (рис. 2).
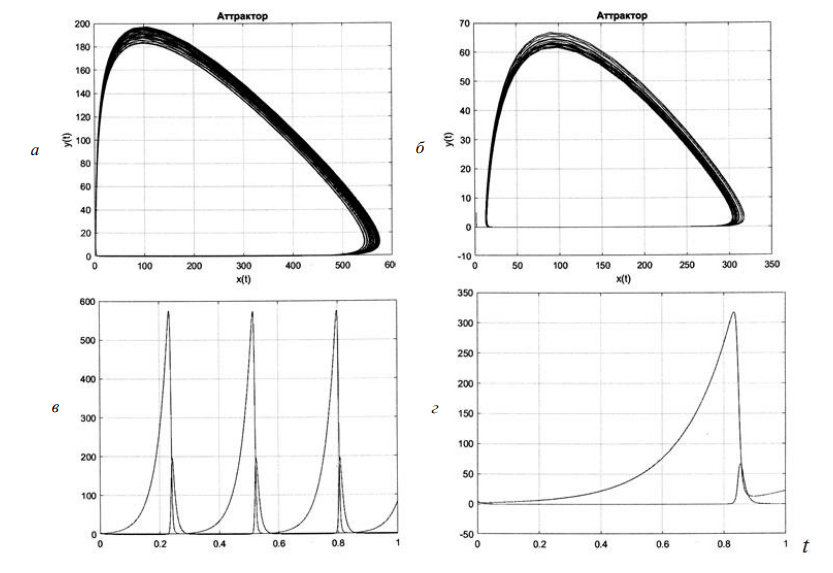
Риc. 2. Динамика системы уравнений (3), (4) при двух значениях коэффициента «k»
и постоянных значениях коэффициентов «c» = 1 и «d» = 100: «k» = 25 (а, в), «k» = 6,25 (б, г);
а, б – аттракторы; в, г – временные характеристики (по оси ординат отложены переменные x(t), y(t)
в относительных единицах)
Fig. 2. Dynamics of the equation system (3), (4) at two values of the coefficient “k”
and constant values of coefficients “c” = 1 and “d” = 100: “k” = 25 (a, в), “k” = 6.25 (б, г);
а, b – attractors; в, г – time characteristics (by ordinate axis placed variable x(t), y(t) in relative units)
Таким образом (см. рис. 1 и 2), при уменьшении «k» в 4 раза (от 100 до 25) максимальная частота автоколебаний уменьшилась с 8,9 до ~ 4 Гц, т. е. в 2 раза (см. рис. 2, в); при уменьшении «k» в 16 раз (до 6,25) частота автоколебаний уменьшилась до ~ 1 Гц (см. рис. 2, г).
Обсуждение
Получены фазовые и временные характеристики управления автоколебаниями лазера как динамической системы на цифровой модели, представленной трехуровневой системой скоростных дифференциальных уравнений. Модель позволяет в широком диапазоне изменения коэффициента управления «d», пропорционального потерям энергии на излучение, исследовать автоколебательный процесс (с регистрацией на фазовой плоскости и на временной развертке) от момента зарождения замкнутой траектории до периодических незатухающих колебаний в форме предельных циклов. В частности, обнаружено появление траектории второй гармоники при малых значениях управляющего коэффициента «d» = 3 («k» = 100, «c» = 1) (см. рис. 1, б, г), которая пропадает с ростом «d»; выявлена зависимость максимальной частоты автоколебаний от накачки (скорости доставки энергии) при остальных неизменных параметрах. Из сравнения длительности синхронных импульсов переменных x(t) и y(t) можно оценить разницу переходных процессов при доставке и расходе энергии для остальных известных параметрах динамической системы. На основе полученных результатов можно полагать, что автоколебательному поведению динамической системы способствует ряд свойств: трех- (и более) уровневая энергетика с квантовыми переходами между уровнями; управление выходными потоками квантов энергии; контроль баланса доставляемой и расходуемой энергии, обеспечивающего стабильность пространственно-временных характеристик системы. Цифровая модель, созданная на основе системы скоростных дифференциальных уравнений лазера, обладает высокой чувствительностью к управлению потерями энергии и позволяет изучить динамику различных по природе динамических объектов при наличии в них энергетических структур.
Заключение
Исследовано управление автоколебаниями лазера как динамической системы в зависимости от внутрирезонаторных потерь излучения. Показано, что при малых потерях излучения, пропорциональных коэффициенту управления «d» (3 % от максимального значения), лазер излучает вторую гармонику, которая пропадает с ростом коэффициента «d». Частота следования импульсов переменных x(t) и y(t) одинакова, но амплитуды импульсов могут отличаться. Могут отличаться и длительности импульсов, например, полуширина импульса переменной y(t) превышает полуширину импульса переменной x(t) в 15 раз (см. рис. 2, г). Отмеченные отличия при автоколебаниях могут быть связаны
с разными как длительностями переходных процессов, так и значениями отношений доставляемой и расходуемой энергии. Предложенная цифровая модель создана на основе трехуровневой лазерной системы скоростных дифференциальных уравнений; для расчетов применен файл sah1064dst.m с встроенной строкой, содержащей оператор @(tx), и решатель ode45. Автоколебательный процесс исследовался детально от момента зарождения замкнутой траектории, появления и ликвидации второй гармоники до периодических незатухающих колебаний в форме предельных циклов. Цифровая модель позволяет вести исследования с регистрацией на фазовой плоскости и временной развертке в широком диапазоне изменения скоростей как доставки, так и потерь энергии. Предложенная цифровая модель позволяет проводить аналогичные исследования на объектах разной природы, в которых имеется энергетическая структура.
Результаты расчетов важны для оптимизации автоматических электроприводов и береговых электроустановок объектов водного транспорта с оптоэлектронными лазерными устройствами.
1. Katanovich A. A., Nikolashin Iu. L. Korabel'nye op-ticheskie sistemy sviazi [Shipboard optical communication systems]. Saint Petersburg, Sudostroenie Publ., 2009. 248 p.
2. Terentyev V. E., Ochina L. B., Belousova I. M., Rusov V. A., Andreev A. A. Opticheskaia generatsiia toka i magnitnogo polia v dinamicheskikh elektrotekhnicheskikh kompleksakh [Optical generation of current and magnetic field in dynamic electrical engineering complexes]. Vestnik Astrakhanskogo gosudarstvennogo tekhnicheskogo universiteta, 2022, no. 2 (74), pp. 38-47.
3. Terentyev V. E. Osobennosti primeneniia mnogomodovykh lazerov v elektroprivodakh [Application features of multimode lasers in electric drives]. Sbornik nauchnyh statec Nacional'noj nauchno-prakticheskoj konferenci professorsko-prepodavatel'skogo sostava FGBOU VO «GUMRF im. adm. S. O. Makarova» (Sankt-Peterburg, 30 sentyabrya – 20 oktyabrya 2024 g.). Saint Petersburg. Izd-vo GUMRF im. adm. S. O. Makarova, 2025. Vol. 3. Pp. 125-129.
4. Terentyev V. E. Lazerno-ul'trazvukovoe kognitivnoe preobrazovanie energii i informatsii v elektroprivode [Laser-ultrasound cognitive transformation of energy and information in an electric drive]. Vestnik Astrakhanskogo gosudar-stvennogo tekhnicheskogo universiteta. Seriia: Upravlenie, vychislitel'naia tekhnika i informatika, 2025, no. 1, pp. 39-45.
5. Airapetian V. S., Ushakov O. K. Fizika lazerov: uchebnoe posobie [Physics of lasers: a textbook]. Novosibirsk, Izd-vo SGGA, 2012. 134 p.
6. Krasil'nikov S. S., Krasil'nikova N. A., Savchenko I. A., Tarasova V. V. Opticheskii kvantovyi generator na rubine. Lazer [Optical quantum generator based on ruby. The laser]. Moscow, UNTs DO Publ., 2005. 55 p.
7. Baryshnikov S. O., Vikhrov N. M., Kuz'min A. A., Sakharov V. V. Komp'iuternye modeli populiatsionnoi dina-miki v ekologicheskikh sistemakh: uchebnoe posobie [Computer models of population dynamics in ecological systems: a textbook]. Saint Petersburg, Izd-vo GUMRF im. adm. S. O. Makarova, 2024. 110 p.
8. Kulikovskaia N. V., Morozov V. M. Attraktor Lorentsa [The Lorentz attractor]. Moscow, Izd-vo MGU im. M. V. Lomonosova, 2022. 23 p.
